УРОК 30
Тема. Решения тригонометрических неравенств
Цель урока: формирование умений учащихся решать тригонометрические неравенства.
И. Проверка домашнего задания.
1. Ответы на вопросы, которые возникли у учащихся при выполнении домашнего задания.
2. Фронтальная беседа с учащимися с использованием рис. 135.
1) дуги соответствуют неравенствам:
tg t > a, tg t a, tg t > a, tg t - a?
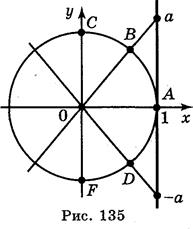
2) Пусть AOB =  . Запишите в виде неравенства дугу, которая соответствует неравенству:
. Запишите в виде неравенства дугу, которая соответствует неравенству:
tg x  a, tg x
a, tg x  a, tg x
a, tg x  - a, tg x
- a, tg x  -a.
-a.
3) Решите неравенства:
tg x  0; tg x
0; tg x 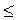 0; ctg x
0; ctg x  0; ctg x
0; ctg x 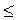 0.
0.
II. Формирование умений решать тригонометрические неравенства
1. Решите неравенства:
а) 2sin 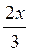
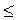 -
- 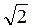 ; б) 2sin
; б) 2sin 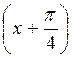
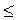 1; в) 3ctg
1; в) 3ctg 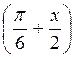 > -
> -  ; г)
; г) 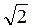 sin
sin 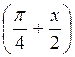
 1.
1.
Ответ: а) 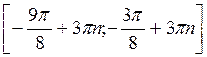 , n
, n Z; б)
Z; б) 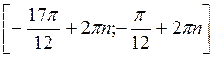 , n
, n Z; в)
Z; в) 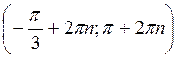 , n
, n Z; г) [4πn; π + 4πn], n
Z; г) [4πn; π + 4πn], n Z.
Z.
2. Решите неравенства:
a) sin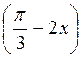 cos
cos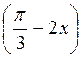
 -
-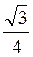 ;
;
б) 2sin2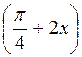
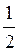 ;
;
в) sin 2x +  cos 2x 0;
cos 2x 0;
г) sin2 x + 2sin x 0.
Ответ: а) 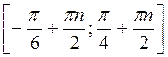 , n
, n Z; б)
Z; б) 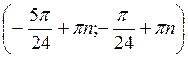 , n
, n Z; в)
Z; в) 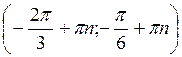 , n
, n Z; г) (-π + 2πn; 2πn), n
Z; г) (-π + 2πn; 2πn), n Z.
Z.
II. Самостоятельная работа
Вариант 1
Решите неравенства:
а) 2sin х - 1. (4 балла)
б) - 3tgx 
 . (4 балла)
. (4 балла)
в) 2 cos 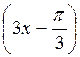
 . (4 балла)
. (4 балла)
Вариант 2
Решите неравенства:
a) 2cosx 
 . (4 балла)
. (4 балла)
б) -  tgx
tgx 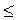 3. (4 балла)
3. (4 балла)
в) 2 sin 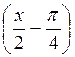
 -1 . (4 балла)
-1 . (4 балла)
Ответ: B-1: a) 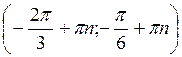 , n
, n Z; б)
Z; б) 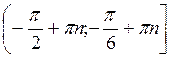 , n
, n Z; в)
Z; в) 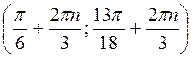 , n
, n Z
Z
B-2: a) 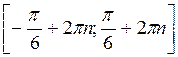 , n
, n Z; б)
Z; б) 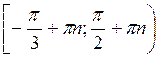 , n
, n Z; в)
Z; в) 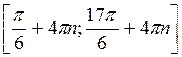 , n
, n Z.
Z.
IV. Обобщение сведений о решении тригонометрических неравенств
Вопрос к классу
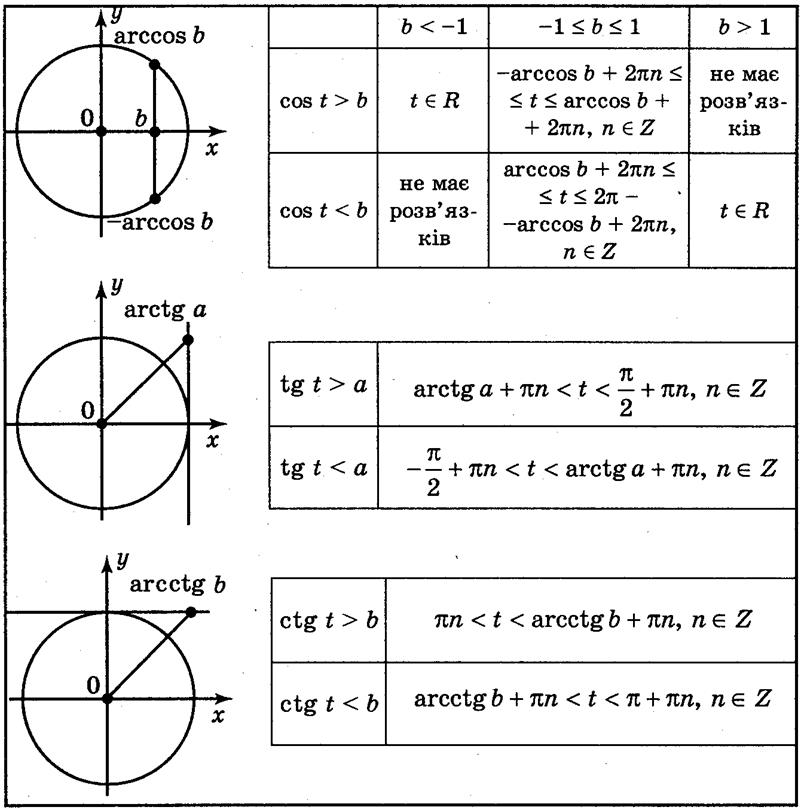
1. При каких значениях а имеет развязки неравенство: a) sin t > а; б) sin t a?
2. При каких значениях b имеет развязки неравенство: a) cos t > b; б) sin t b?
3. Как найти развязки неравенств: a) sin t > а; б) sin t а; в) cos t > b; г) cos t b?
4. Как найти развязки неравенств: a) tg t > а; б) tg t а; в) ctg t > b; г) ctg t b?
В ходе обсуждения вопросов заполняется таблица 12 на доске и в тетрадях учащихся.
V. Подведение итогов урока
VI. Домашнее задание
Решите неравенства:
a) sin 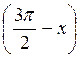
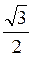 ; б) cos2
; б) cos2 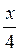 - sin2
- sin2 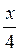
 - 0,5; в) sin х +
- 0,5; в) sin х +  cos х > 0 .
cos х > 0 .
Таблица 12