УРОК 29
Тема. Решение простейших тригонометрических неравенств
Цель урока: формирование умений учащихся решать простейшие тригонометрические неравенства: tg t > a, tgt a, ctg t a, ctg t > a (tgt  a, tgt
a, tgt 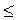 a, ctg t
a, ctg t 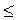 a, ctg t
a, ctg t  a).
a).
И. Проверка домашнего задания
1. Ответы на вопросы, которые возникли у учащихся в процессе выполнения домашних заданий.
2. Фронтальная беседа с учащимися с использованием рис. 130.
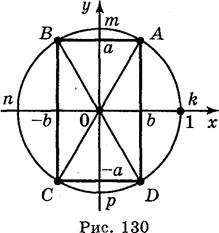
1) Какая дуга соответствует неравенствам: sin t > a; cos t > b; sin t > - a; cos > - b; sin t a, cos t b, sin t - a, sin t - b?
2) Решением которой неровности есть дуга АmВ; AkD; CpD; Сn?
3) Решите неравенства: cos t  1; sin t > 5; sin t 5; sin t -1; cos t >π; cos t π; cos t
1; sin t > 5; sin t 5; sin t -1; cos t >π; cos t π; cos t  0; cos t
0; cos t 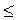 0; sin t
0; sin t  0; sin t
0; sin t 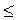 0.
0.
II. Восприятие и осознание решения простейших тригонометрических неравенств
На сегодняшнем уроке мы продолжим учиться решать простейшие тригонометрические неравенства.
Рассмотрим примеры.
Пример 1. Решите неравенство tg t 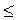 1.
1.
Решение
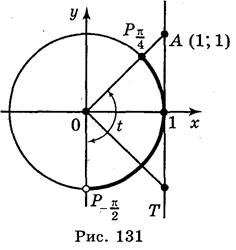
Построим единичный круг и линию тангенсов (рис. 131). На оси тангенсов обозначим число 1. Если t является решением неравенства, то ордината точки Т, равна tg t, должна быть не больше 1. Множество таких точек Т - луч AT. Множество точек 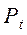 , соответствующих точкам луча АО, - дуга
, соответствующих точкам луча АО, - дуга 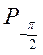
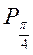 , которая на рисунке выделена. (Обратите внимание: точка
, которая на рисунке выделена. (Обратите внимание: точка 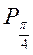 принадлежит, а точка
принадлежит, а точка 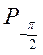 не принадлежит множеству решений). Следовательно, решением неравенства будут все значения t из промежутка
не принадлежит множеству решений). Следовательно, решением неравенства будут все значения t из промежутка 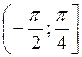 . Учитывая, что период функции tg t равна π, имеем решение данной неровности
. Учитывая, что период функции tg t равна π, имеем решение данной неровности 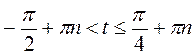 , n
, n Z.
Z.
Ответ: 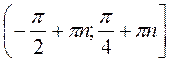 , где n
, где n Z.
Z.
Пример 2. Решите неравенство tg t > 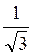 .
.
Решение
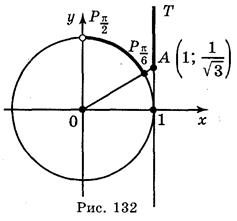
На оси тангенсов (рис. 132) обозначим число 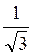 и множество значений тангенсов, не меньше
и множество значений тангенсов, не меньше 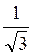 (луч AT). На единичной окружности множество точек, соответствующих углам, тангенс которых не меньше
(луч AT). На единичной окружности множество точек, соответствующих углам, тангенс которых не меньше 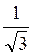 , есть дуга
, есть дуга 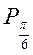
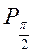 . Следовательно, решением неравенства будут все значения t из промежутка
. Следовательно, решением неравенства будут все значения t из промежутка 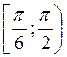 . Учитывая периодичность, имеем:
. Учитывая периодичность, имеем: 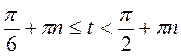 , где n
, где n Z.
Z.
Ответ: 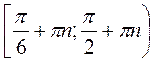 , где n
, где n Z.
Z.
Пример 3. Решите неравенство ctgt  -
-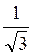 .
.
Решение
1 способ. Учитывая, что ctg t = tg 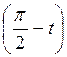 , имеем ctg t = - tg
, имеем ctg t = - tg 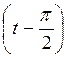 , тогда имеем неравенство-tg
, тогда имеем неравенство-tg 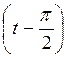
 -
- 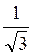 a6o tg
a6o tg 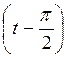
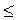
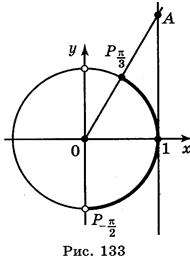
 . Решим последнее неравенство (рис. 133), имеем:
. Решим последнее неравенство (рис. 133), имеем: 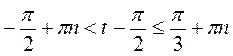 , n
, n Z;
Z; 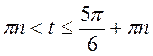 , n
, n Z.
Z.
Ответ: 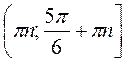 , где n
, где n Z.
Z.
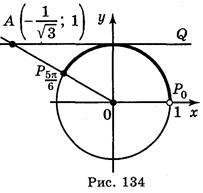
2 способ. На оси котангенсів обозначим число и множественное число (рис. 134) значений котангенсів, не меньше -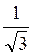 (луч AQ). На единичной окружности множество точек, соответствующих углам, котангенс которых не меньше -
(луч AQ). На единичной окружности множество точек, соответствующих углам, котангенс которых не меньше -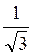 есть дуга
есть дуга 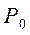
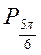 Следовательно, решения неравенства будут все значения t из промежутка
Следовательно, решения неравенства будут все значения t из промежутка 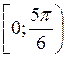 . Учитывая периодичность, имеем:
. Учитывая периодичность, имеем: 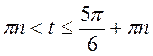 , n
, n Z.
Z.
Ответ: 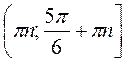 , где n
, где n Z.
Z.
III. Формирование умений решать простейшие неравенства
1. Решите неравенства: a) tg x  - 1; б) tg x
- 1; б) tg x 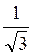 ; в) tg x
; в) tg x  2; г) ctg х >
2; г) ctg х >  .
.
Ответ: а) 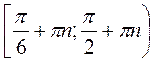 , n
, n Z; б)
Z; б) 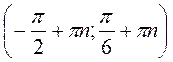 , n
, n Z; в)
Z; в) 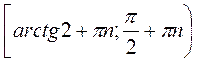 , n
, n Z; г)
Z; г) 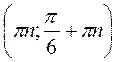 , n
, n Z.
Z.
IV. Подведение итогов урока
V. Домашнее задание
Раздел II § 5. Вопросы и задания для повторения раздела II № 24. Упражнение№ 3 (2, 4, 6, 8).