Перпендикуляр

Две прямые называются перпендикулярными, если они пересекаются под прямым углом (см. рисунок), то есть, когда они пересекаются, образуются четыре прямых угла.
Обозначения: .

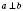
Теорема 1. Через каждую точку прямой можно провести перпендикулярную к ней прямую, и только одну.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной прямой, который имеет одним из своих концов их точку пересечения.
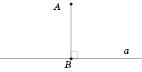
На рисунке AB - перпендикуляр, проведенный из точки A к прямой a. Точка B называется основанием перпендикуляра.
Обозначения: .

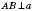
Теорема 2. С любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Обратите внимание: теорема содержит два утверждения - существование перпендикуляра и его единственность.