АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел III. ФУНКЦИЯ

§14. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ.

3. Свойства арифметической прогрессии.

Рассмотрим свойства арифметической прогрессии.

1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов, то есть

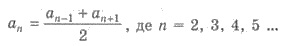
2. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух равноотстоящих членов, т.е.

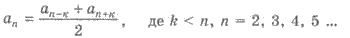
3. Если k, l, р и s - натуральные числа, такие, что k + l = г + s, то

4. Любую арифметическую прогрессию можно задать формулой а_n = dn + b, где d и b - некоторые числа.

5. Последовательность а_n, заданная формулой n-го члена а_n = dn + b, где d и b - некоторые числа, является арифметической прогрессией.