Часть 1 МЕХАНИКА

Глава 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.18. Математический маятник

Математический маятник является физическим абстракция, под которой понимают точечное тело, подвешенное на упругой бесконечно длинной и воздушном нитке. Практическим приближением к математическому маятнику будет система, состоящая из шара и подвеса, при этом диаметр шара значительно меньше от длины нити, к которой подвешен.

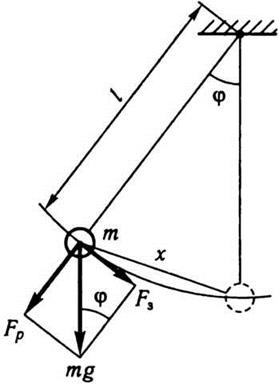
Рис. 2.12

Пусть смещение маятника будут небольшие. Как видно из рис. 2.12, обратная сила в этом случае равна F₃ = mg sin φ. Сила тяжести mg в таком положении маятника, когда он отклонился от первоначального положения на угол φ, раскладывается на две составляющие: обратную силу, возвращает маятник в предыдущее положения, и составляющую, которая направлена вдоль нити и уравновешивается реакцией нити. Следовательно, обратная сила

Из рис. 2.12. видно, что sin φ = x/l. Тогда

где с = mg /l. Период Т гармонических колебаний связан с коэффициентом обратной силы с так:

Подставим в (2.70) значение с для математического маятника. Тогда

Из соотношения (2.71) следует, что период колебаний математического маятника зависит не от его массы, а от его длины и ускорения свободного падения.

Итак, с помощью математического маятника можно определить ускорение свободного падения g. Оно зависит от географической широты местности и пород, залегающих в ней.