Часть 1 МЕХАНИКА

Глава 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.17. Колебания. Гармонические колебания

Колебаниями называют процессы, происходят с точным или приближенным повторением состояний системы. Такая повторяемость свойственна, например, колебания маятника часов, колебания струны, изменении напряжения между обкладками конденсатора в контуре радиоприемника и т.д.

В зависимости от физической природы процесса, что повторяется, различают колебания механические, электромеханические, электромагнитные и т.д. В этом разделе рассмотрим механические колебания.

В зависимости от характера действия на систему, которая колеблется, различают свободные (или собственные), вынуждены, параметрические колебания и автоколебания. Простейшими являются гармонические колебания, то есть такие, когда значение изменяется при колебаниях (например, отклонение маятника от положения равновесия), изменяется со временем по закону синуса или косинуса. Этот вид колебаний важно рассмотреть по следующим причинам: во-первых, колебания, наблюдаемые в природе и технике, по своему характеру приближаются к гармоничным, а, во-вторых, периодические процессы иной формы (с другой зависимостью от времени) можно представить как наложение нескольких гармонических колебаний. Колебательное движение имеет особенно простой характер тогда, когда обратная сила увеличивается пропорционально смещению от положения равновесия тела, что колеблется. Именно в этом случае происходят гармонические колебания.

Рассмотрим гармонические колебания чисто тематически. Пусть точка В (рис. 2.10) движется по окружности радиуса а с постоянной угловой скоростью ω. Проследим за движением точки С (В проекции на вертикальную ось). В момент времени t = 0 радиус ВB занимал положение ОА. Тогда в момент времени t радиус ОВ вернется из начального положения ОА на угол φ. Смещение х точки С, равна отрезка ОС, определяется так:

Угол φ называют фазой колебания точки С.

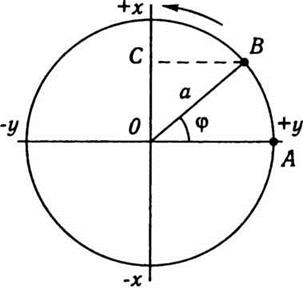
Рис. 2.10

Если 2π является длиной дуги полного круга в угловых единицах, а Т - время обхода точкой В полного круга, то угловая скорость равна

Величину ω называют круговой, или циклической, частотой. Отсюда нетрудно выразить фазу φ через ω:

Подставив это значение фазы в уравнение (2.59), получим

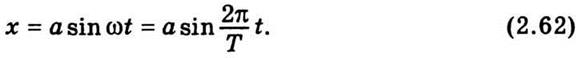
Рассматривая изменение проекции точки В на горизонтальную ось, аналогично получим

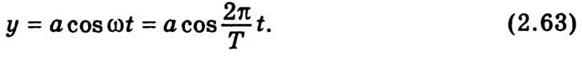
Колебательный характер движения, выраженного уравнениями (2.62) и (2.63), становится особенно наглядным, если представить их графически, как это сделано на рис. 2.11. Колебательное движение, которое описывается функцией синуса или косинуса, называется простым гармоничным колебанием. Это движение полностью определяется следующими величинами: 1. Амплитудой а - расстоянием наибольшего отклонения от начального положения. 2. Периодом колебаний Т, то есть время, в течение которого точка (тело), что колеблется, осуществит полный цикл колебательного движения, смещаясь сначала в одну, а затем в другую сторону от начального положение и снова возвращаясь к нему. Вместо периода колебаний можно задать его частоту ν, определяется количеством полных колебаний за 1 с. За единицу частоты взято 1 герц (Гц) - это частота такого колебания, период которого равен 1 с. Период и частота связаны между собой так:

Круговая частота ω равна количеству полных колебаний за 2π секунд:

Определим силу, под действием которой будут возникать простые гармонические колебания. Для этого воспользуемся, например, уравнение (2.62) и найдем сначала скорость υ и ускорение W точки, гармонично колеблется:

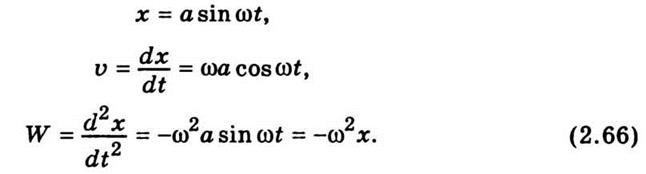
Умножив левую и правую части уравнение (2.66) на массу материальной точки, получим дифференциальное уравнение простого гармонического колебания:

где с = mω² - коэффициент обратной силы. Итак, тело осуществлять простое гармоническое колебание, если на него будет действовать обратная сила, пропорциональна смещению тела от положения равновесия. Гармоническое колебание - это движение, вызванное силой, что изменяется пропорционально отклонению х тела от положение равновесия. Сила F = -сх полностью характеризует колебания тела вблизи положения равновесия, т.е. при малых амплитудах колебания. С увеличением амплитуды колебаний может наступить ангармонічність и пропорциональность между обратной силой и смещением тела нарушается.

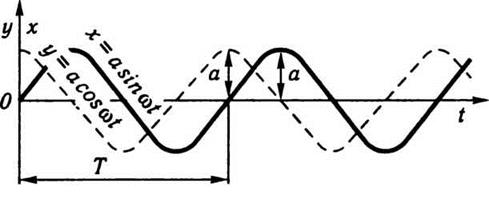
Рис. 2.11