ПРИМЕНЕНИЕ ЗАКОНОВ ДИНАМИКИ

Урок № 19

Тема. Закон сохранения механической энергии

Цель: раскрыть сущность закона сохранения энергии в механических процессах; расширить представление учащихся о сфере использования закона сохранения энергии; научить их применять свои знания для решения соответствующих задач.

Тип урока: комбинированный.

План урока

Самостоятельная работа «Энергия»

Начальный уровень

1. Какие из перечисленных тел обладают потенциальной энергии: а) шар, катится по земле; б) лук с натянутой тетивой; в) сжатый в баллоне газ; г) кабинка «колеса обозрения»?

2. Опишите превращения энергии, которые происходят в ходе спортивной стрельбы из лука.

Средний уровень

1. Камень, брошенный с поверхности земли со скоростью 10 м/c, в верхней точке траектории имел кинетическую энергию 5 Дж. Определите массу камня.

2. Тело массой 1 кг находится на высоте 2 м от поверхности земли. На какой высоте следует расположить тело массой 0,5 кг, чтобы оно имело такую же потенциальную энергию?

Достаточный уровень

1. Найдите потенциальную и кинетическую энергии тела массой 3 кг, падающего свободно с высоты 5 м, на расстоянии 2 м от поверхности земли.

2. Камень массой 5 кг упал с некоторой высоты. Найдите кинетическую энергию камня в средней точке его пути, если он падал в течение 2 с.

Высокий уровень

1. Определите кинетическую энергию тела массой 1 кг, брошенного горизонтально со скоростью 20 м/c, в конце четвертой секунды его движения.

2. Кусок льда один раз бросают под углом 45° к горизонту, а второй раз пускают с такой же скоростью скользить по льду. Найдите коэффициент трения, если во втором случае кусок льда переместился на расстояние, в 10 раз большую, чем в первом случае.

Изучение нового материала

1. Изменение потенциальной и кинетической энергии во время свободного падения

Из предыдущих уроков ученикам известно, что при взаимодействии тел их энергия меняется, причем в одних случаях кинетическая энергия тела увеличивается вследствие роста его скорости, в других - уменьшается вследствие уменьшения скорости. Так же может меняться и потенциальная энергия.

Следует обратить внимание на то, что любое тело одновременно как потенциальную, так и кинетическую энергию. Эти виды энергии в механических процессах могут взаимно превращаться. Такие преобразования можно рассмотреть на примере свободного падения тела.

2. Закон сохранения механической энергии

Пусть груз массой m падает без начальной скорости с высоты H (см. рис.).

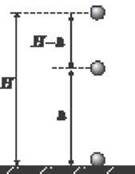
Рис. 1

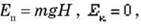
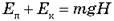
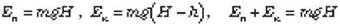
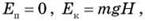
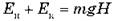
В начальный момент времени на высоте Н потенциальная энергия равна Еп = mgh, а кинетическая - Ек = 0. В момент удара груза о землю потенциальная энергия равна Еп = 0, а кинетическая - Eк = m2/2, где 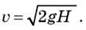Тогда Ек = mgH.

Чему равна сумма потенциальной и кинетической анергій на промежуточной высоте hH?

Потенциальная энергия Еп = mgH, а чтобы найти кинетическую энергию Eк = m2/2, следует воспользоваться формулой 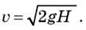, где l - путь, пройденный грузом. Поскольку l = H - h, получим:

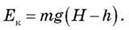
Следовательно, Еп + Ек = mgh + mg (H - h) = mgH = const, т.е. сумма потенциальной и кинетической энергий является величиной постоянной.

На примере колебаний маятника (или маятника Максвелла) также можно показать превращение потенциальной энергии в кинетическую и наоборот.

Далее можно разобрать с учениками такой вопрос: так ли это утверждение в случае упругого взаимодействия?

Рассмотрев движение бруска, прикрепленного к пружине, получим, что и для системы, в которой действуют силы упругости, полная механическая энергия сохраняется неизменной, т.е.

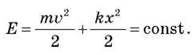
Если одно из слагаемых полной энергии увеличивается на определенную величину, то второе слагаемое уменьшается на такую же величину.

На основании рассмотренных примеров необходимо подвести учащихся к формулировке одного из важнейших законов сохранения в природе - закона сохранения механической энергии:

если между телами замкнутой системы действуют только силы тяготения и силы упругости, механическая энергия системы сохраняется:

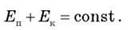
Если, кроме сил тяготения и упругости, между телами системы действует сила трения скольжения, механическая энергия уменьшается. В результате действия силы трения скольжения тела нагреваются, то есть механическая энергия частично переходит во внутреннюю энергию.

Структурным принципом всего курса механики средней школы является решение основной задачи механики, поскольку именно эта задача определяет содержание и структуру всей совокупности необходимых понятий. Динамический способ решения основной задачи механики требует знания сил, действующих на тело в любой момент времени. Когда происходят реальные взаимодействия, значения этих сил известны не всегда. В таких случаях применяется энергетический способ решения. Кроме того, энергетический способ часто дает более рациональное решение и в тех случаях, когда применяют динамический способ решения основной задачи механики. Ряд задач можно решить только в результате применения обоих законов сохранения (импульса и энергии).

Вопрос к учащимся в ходе изложения нового материала

1. Что показывает энергия тела?

2. Что называют полной механической энергией?

3. Груз, подвешенный к пружине, совершает колебания в вертикальном направлении. Какие превращения энергии при этом происходят? Которыми являются положения бремени, когда потенциальная энергия системы «груз и пружина» максимальная?

4. Тело соскальзывает по наклонной плоскости так, что его скорость остается неизменной. Меняется ли при этом полная механическая энергия тела? Какие превращения энергии при этом происходят?

5. Почему в случае действия силы трения закон сохранения механической энергии нарушается?

Качественные задачи

1. Почему трудно прыгнуть на берег из лодки, а такой же прыжок с теплохода осуществить легко?

2. Упав с высоты 2 м, мячик подскочил на высоту 1,5 м. Как согласовать это с законом сохранения энергии?

3. Камень и теннисный мяч бьют палкой. Почему мяч при прочих равных условиях летит дальше, чем камень?

4. Резиновые баллоны автомашины (а также рессоры, вагонные буфера и т.д.) ослабляют толчки и удары. Почему?

5. Деревянный кубик был привязан к камню на дне озера. Веревка порвалась, и кубик истек. Как изменилась в результате этого потенциальная энергия системы «кубик + вода + Земля»? (Ответ: уменьшилось.)

Задачи, решаемые на уроке

1. Тело, брошенное под углом к горизонту, побывало на высоте 20 м дважды. Можно утверждать, что скорость тела была при этом одинаковой? А модуль скорости? Считайте, что сопротивлением воздуха можно пренебречь.

2. Камень бросили с земли под углом к горизонту, придав ему начальную скорость 0 = 15 м/c. Какой была скорость камня на высоте h = 10 м?

Дано: 0 = 15 м/c, h = 10 м, g = 9,8 м/c2.

Найти: - ?

Решение

Кинетическая энергия камня сразу после броска 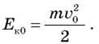На высоте h камень имеет потенциальную энергию Еп = mgh и кинетическую энергию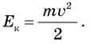

При отсутствии силы сопротивления воздуха полная механическая энергия сохраняется:

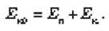
Из уравнения 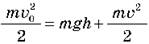имеем: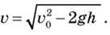

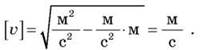
Ответ: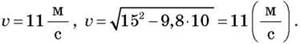

3. Тело свободно падает с высоты 15 м над землей. Какую скорость оно обладает в тот момент, когда его кинетическая энергия равна потенциальной?

4. Камень брошен вертикально вверх со скоростью 10 м/c. На какой высоте кинетическая энергия камня равна его потенциальной энергии?

5. В брусок, висящий на шнуре длиной l = 2 м, попала пуля из стрелкового оружия, которая летела горизонтально. Пуля застряла в бруске. С какой скоростью 0 летела пуля, если шнур отклонился от вертикали на угол α = 15°? Масса бруска М = 2 кг , масса пули m = 8 г.

Дано: l = 2 м, α = 15°, Г = 2 кг, m = 8 г= 0,008 кг

Найти: 0

Решение

Процесс можно разбить на два этапа. Первый этап - столкновение пули с бруском. При этом брусок набирает скорости u , но практически не успевает сдвинуться с места. Механическая энергия не сохраняется, но сохраняется импульс: m0 = (M + m)u.

На втором этапе процесса брусок с застрявшей в нем пулей отклоняется на угол а, поднимаясь при этом (рис. 2) на высоту h = l(1 - cosα).

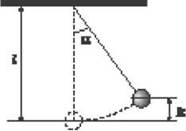
Рис. 2

На этом этапе механическая энергия сохраняется:

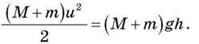
Отсюда:

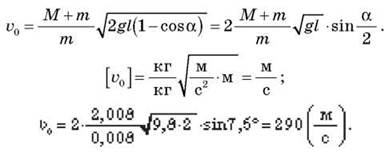
Ответ: 0 = 290 м/c.

Домашнее задание

1. С какой скоростью надо бросить вниз мяч с высоты 1 м, чтобы после упругого удара о площадку он «подпрыгнул» на высоту 4 м?

2. Подайте кинетическую энергию тела через его массу m и импульс p.

3. Камень брошен вертикально вверх со скоростью 15 м/c. На какой высоте его кинетическая энергия в 2 раза превышает потенциальную энергию?