Урок № 27
Тема. Одночлен умножение. Подъем одночлен в степень
Цель: добиться сознательного понимания алгоритмов преобразования произведения и степени одночлена в одночлен стандартного вида; продолжить формирование навыков выполнения действий со степенями.
Тип урока: усвоение знаний; формирования навыков.
Ход урока
I. Проверка домашнего задания
Блиц-контроль
1. Из выражений является одночленом: 1) 3 + х2; 2) 3х2; 3) 3 : х2; 4) (х - 3)2?
2. Из записей является одночленом стандартного вида:
1) х2 ∙ в ∙ 3у2; 2) 3х2 ∙ в ∙ 2; 3) 6х2у; 4) 6 - х2у?
3. Назовите коэффициент и степень одночлена: 3х2у3z (в указанном порядке):
1) 3; 2; 2) 3; 5; 3) 3; 3; 4) 3; 6.
@ Во время коррекции выполненной работы очень важно побуждать учащихся к обоснованию своего выбора.
II. Актуализация опорных знаний
1. Упростите выражение: хх3 х5 х0; р18 : р3; (m ∙ m3)6.
2. Найдите значение выражения при х = -2:
5х2; -5х2; 5(-х)2; 2х2; -2х3; 2(-х)3.
3. При каких значений является правильной неравенство: у2 ≤ 0, у2 > 0?
III. Работа с опережающим домашним заданием
@ На доске записаны примеры (из учебника или аналогичные) на одночлен умножение и возведение одночлена в степень.
1. -3а2b ∙ 4аb3 = (-3 ∙ 4) ∙ (а2 ∙ а) ∙(b ∙ b3)= -12а3b4.
2. (-5а2b)3 = (-5)3 ∙ (а2)3 ∙ b3 = -125а6b3.
Ученикам предлагаем прокомментировать каждый шаг в проводимых преобразованиях, а именно: какие понятия, их свойства было использовано (желательно эти свойства и понятия визуализировать, то есть во время комментариев делать записи на доске).
IV. Усвоение знаний
@ После проведенной работы с домашним заданием будет уместным сделать выводы - сформулировать алгоритмы преобразования произведения и степени одночлен одночлена в виде одночлена стандартного вида (можно предложить выполнить эту работу ученикам).
Единственное, о чем можно поговорить или вынести на следующий урок,- Это случаи, когда надо преобразовать выражение, содержащее и умножения одночлен, и возведение одночлена в степень (напомнить учащимся о последовательности выполнения действий разной степени).
V. Применение знаний. Формирование и совершенствование умений
@ Поскольку на изучение вопроса, внесенного в тему урока, отводится два урока, первый урок мы посвятим закреплению знаний содержания алгоритмов одночлен умножение и возведение одночлена в степень и совершенствованию приобретенных умений выполнять прямые и обратные преобразования (то есть произведение одночлен в одночлен и представление одночлена в виде произведения двух или нескольких множителей; преобразование степень одночлена в одночлен стандартного вида и представление одночлена в виде степени).
Выполнение устных упражнений
1. Перемножте одночлен: 1) 2а и 3b; 2) 4с2 и 2с; 3) 5a2b и ab; 4) - ху2 и 2х.
2. Возведите в степень одночлен: 1) (2а)2; 2) (2а -b)3; 3) (-2а2)3; 4)(-а2b)3.
Выполнение письменных упражнений
1. Выполните умножение одночлен:
1) 4х ∙ 7у;
2) -8х ∙ 5х3;
3)  аb3 ∙
аb3 ∙ 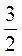 аb;
аb;
4) 0,2m3n9 ∙ 2,5m4n;
5) 0,75а9b3с2 ∙ 1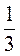 а4bс7;
а4bс7;
6) 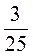 m4с9 ∙(-10mа) ∙ 2,5с3а6;
m4с9 ∙(-10mа) ∙ 2,5с3а6;
7*) 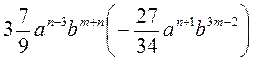 .
.
2. Подайте одночлен - 12х4у3 двумя способами в виде произведения:
1) двух одночлен стандартного вида;
2) трех одночлен стандартного вида;
3) четырех одночлен стандартного вида.
3. Возведите в степень:
1) (3x2)3;
4. 2) (4m)2;
5. 3) (-3xв2)3;
6. 4) (-0,2a7b3c)2;
5) 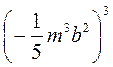 ;
;
6) 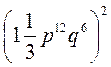 ;
;
7*) 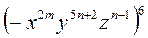 .
.
7. Представьте одночлен в виде квадрата одночлена:
1) 16а2; 2)25а8; 3) 64а10b6; 4) 0,36m12n4; 5) 729х14у8z24.
8. Представьте одночлен в виде куба одночлена:
1) 27а3; 2) 64а9; 3) -125а6b15; 4) 0,008х6у8; 5) -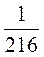 а21b33с6.
а21b33с6.
VI. Итоги урока. Рефлексия
Правильно выполнены преобразования выражений:
1) 2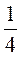 a5b ∙
a5b ∙ 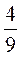 a3b = 2
a3b = 2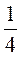 (a5a3)(bb) = 2
(a5a3)(bb) = 2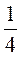 a8 ∙ 2b;
a8 ∙ 2b;
2) (-2a2b)3 = (-2)3a3b3 = 8a3b3?
Найдите и исправьте ошибку.
VII. Домашнее задание
№ 1. Выполните умножение одночлен:
l) 0,4a3b5 ∙ 1,5а3b;
2) 0,45m3n2р4 ∙ 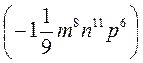 ;
;
3) 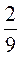 а5с ∙ (15b3с2) ∙ 1,2а3b6;
а5с ∙ (15b3с2) ∙ 1,2а3b6;
4) 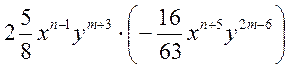 .
.
№ 2. Возведите в степень:
1) (2х3у)3;
2) (-5а4b2с3)2;
3) 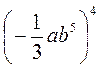 ;
;
4) (13x5у6z7)2;
5) 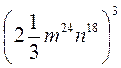 ;
;
6) (-а2n b3n-1 cn+2)10.
№ 3. Опережающее домашнее задание. Сравните выражение
1) 5а6 ∙ (-3а2b)2 с выражениями 2) 5а6 ∙ 9а4b2 и 3) (-3а2b)2
(по алгоритму сравнения).
Какие действия и в каком порядке нужно выполнить, чтобы упростить выражение 1)?