УРОК № 28

Тема. Уравнение прямой

Цель урока: вывод уравнения прямой. Формирование умений учащихся использовать уравнение прямой к решению задач.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Декартовы координаты и векторы на плоскости» [13].

Требования к уровню подготовки учащихся: записывают и объясняют уравнение прямой. Распознают уравнение прямой.

Ход урока

I. Проверка домашнего задания

Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учеников во время их выполнения.

II. Анализ результатов самостоятельной работы

III. Восприятие и осознание нового материала

Докажем, что любая прямая в декартовых координатах имеет уравнение ax + by + c = 0, где а, b, с - некоторые числа, а х и у - переменные координаты точки А(х; у), принадлежащей прямой.

Как и при составлении уравнения круга, обратимся к такого свойства прямой, которые имеют точки этой прямой, то есть: точки, равноудаленные от двух данных точек В и С, лежат на прямой (срединном перпендикуляре к отрезка ВС), которая перпендикулярна к ВС и проходит через середину отрезка ВС.

Пусть h - произвольная прямая на плоскости и А(х; у) - точка этой прямой. Проведем какую-нибудь прямую, перпендикулярную к прямой h, и отложим на ней от точки D пересечения с прямой h равные отрезки (рис. 143) BD и DC, где B(a1; b1), С(а2; b2).Оскільки АВ = АС, тогда АВ2 = АС2, или (x - a1)2 + (y - b1)2 = (x - a2)2 + (y - b2)2.

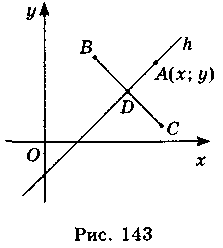
Упростим эту равность:

х2 - 2ха1 + 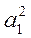+ у2 - 2yb1 + 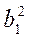= х2 - 2ха2 + 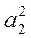+ у2 - 2уb2 + 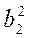, или-2хa1 + 2ха2 - 2yb1 + 2yb2 + 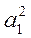+ 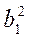- - 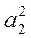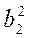= 0,

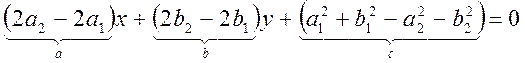, тогда имеем

ax + by + с = 0, где а = 2а2 - 2а1, b = 2b2 - 2b1, c = + - - .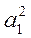

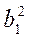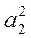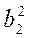Следовательно, уравнение прямой имеет вид ах + bу + с = 0, где a, b, c - некоторые числа.

Решение упражнений

1. 1) Найдите координаты точек пересечения с осями координат прямой:

а) 2х - 3y = 6;

б) -3х - 7у = 21;

в) 4х + 3y - 12 = 0.

1. 2) Прямая задана уравнением 2х + у - 1 = 0. Какие из точек А(0; 0), В(1; -1), С(0; 1), D(1; 0) принадлежат прямой, а какие не принадлежат ей?
2. 3) Постройте прямые:

а) 2x - y + l = 0;

б) - х + 2у + 2 = 0;

в) х + у - 1 = 0.

IV. Закрепление и осмысление нового материала

Решение задач

1. 1. Запишите прямой, проходящей через точку А(3; 4), которая:
   а) параллельна оси Ох;

б) параллельна оси Оу;

в) проходит через начало координат.

1. 2. Известно, что прямая у - ах - 3 = 0 проходит через точку А(-1; 1). Найдите значение а.
2. 3. Запишите уравнение прямой АВ, если А(2; 3), В(3; 2).

Решение

Поскольку искомая прямая ах + bу + с = 0 проходит через точки А и В, то

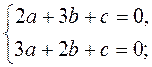
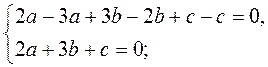
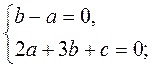
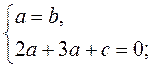
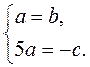
Пусть с = -5, тогда а = 1, b = 1. Следовательно, х + у - 5 = 0 - уравнение искомой прямой.

Ответ, х + у - 5 = 0.

1. 4. Концы диаметра А и В окружности имеют координаты А(-3; 2), В(1; 7). Составьте уравнение прямой, проходящей через центр окружности и перпендикулярна к диаметру. (Ответ. 8х + 10y - 37 = 0)
2. 5. Докажите, что окружность (х + 2)2 + (y - 3)2 = 52 имеет с прямой х - 2у = 6 две общие точки. Найдите эти точки. (Ответ. (4; -1) и (-2,4; -4,2))

V. Домашнее задание

1. 1. Изучить уравнение прямой.
2. 2. Решить задачи.
3. 1) Составить уравнения прямых, которые проходят через точки:

а) А(0; 0) и В(1; 1);

б) A(-3; 2) и В(-2; 1).

1. 2) Построить прямые:

а) х + 2у - 3 = 0;

б) х - 5 = 0;

в) 2у + 4 = 0.

VI. Подведение итогов урока

Задача класса

1. 1. Запишите уравнение прямой в общем виде. Какие данные надо знать, чтобы записать уравнение прямой? Запишите уравнение прямой, если а = -2, b = 3, с = 6.
2. 2. Определите, как расположена на координатной плоскости прямая:

а) x + 5 = 0;

б) y - 1 = 0;

в) х = 0;

г) y = 0.