Урок 28

Тема. Решение задач на применение признака перпендикулярности прямой и плоскости

Цель урока: формирование умений учащихся применять определение и признак перпендикулярности прямой и плоскости к решению задач.

Оборудование: стереометрический набор, модель куба.

Ход урока

И. Проверка домашнего задания

1. Проверка правильности решения задачи № 7 по записям (с пробелами), сделанными на доске до начала урока.

Решение задачи № 7

Пусть ABCD - прямоугольник; КА ...(АВС);

KB = 7 м, КС = 9 м, KD = 6 м (рис. 144).

С ΔКВА АВ = = = .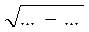

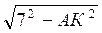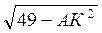С ΔКAD AD = = .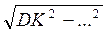

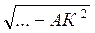С ΔАСD AC2 = AD2 + DC2 = AD2 +... = 36 - АК2 + + 49 - АК2 = ... - 2АК2.

Из ΔАСK КС2 = АК2 + АС2; ... = АK2 + 85 - АК2; АК2 = 85 - ...; АК2 = 4 ; АК = 2 (м). Ответ. 2 м.

2. Математический диктант.

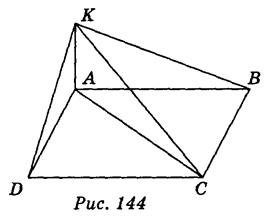
Отрезок МА перпендикулярен к плоскости АВС:

Вариант 1 - прямоугольника ABCD (рис. 145);

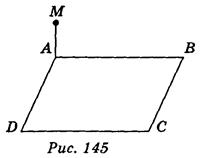
Вариант 2 - ромба CBDF (рис. 146), в котором АВ = 3 см, AD = 4 см, МА = 1 см.

Пользуясь рисунком, найдите:

1) расстояние между точками М и В; (2 балла)

2) длину отрезка MD; (2 балла)

3) расстояние между точками А и С; (2 балла)

4) длину отрезка BD; (2 балла)

5) расстояние между точками М и С; (2 балла)

6) площадь треугольника МАСС. (2 балла)

Ответ. Вариант 1. 1) 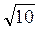см; 2) 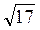см; 3) 5 см; 4) 5 см; 5) 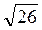см; 6) 2,5 см2.

Вариант 2. 1) 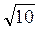см; 2) 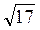см; 3) 4 см; 4) 5 см; 5) 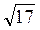см; 6) 2 см2.

II. Закрепление и осмысление знаний учащихся

Решение задач

1. Три луча ОА, ОВ и ОС попарно перпендикулярны. Как расположен каждый из лучей относительно плоскости, определяемой двумя другими лучами?

2. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОК, перпендикулярную к плоскости квадрата. Найдите расстояние от точки к до вершин прямоугольника, если ОК = b.

(Ответ. )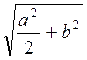

3. В треугольнике ABC C = 90°, AC = 6 см, ВС = 8 см, CM - медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК =12 см. Найдите KM.

(Ответ. 13 см)

4. Прямая CD перпендикулярна к плоскости правильного треугольника АВС. Через центр О этого треугольника проведена прямая ОК, параллельная прямой CD. Известно, что АВ = 16см, ОК = 12см, CD = 16см. Найдите расстояние от точек D и к до вершин А и В треугольника.

(Ответ. КА = КВ = 20 см; DA = DB = 32 см)

5. Ребро куба равно а. Найдите расстояние от точки пересечения диагоналей одной из граней к вершинам противоположной ей грани.

(Ответ. 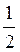a)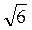

6. Диагональ BD1 прямоугольного параллелепипеда ABCDA1B1C1D1 равна d, диагональ AD1 грани равна b. Найдите АВ.

(Ответ. )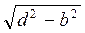

7. Задача № 5 из учебника (с. 34).

III. Домашнее задание

§3, п. 15; задача № 8 (с. 35).

IV. Подведение итога урока

Вопрос к классу

1) Дайте определение прямой, перпендикулярной к плоскости.

2) Сформулируйте признак перпендикулярности прямой и плоскости.

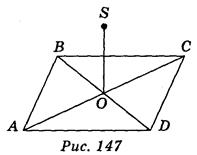
3) Расстояние от точки S до каждой из вершин прямоугольника ABCD равна (рис. 147), точка О - точка пересечения диагоналей АС и BD прямоугольника ABCD. Укажите, какие из приведенных ниже утверждений правильные, а какие - неправильные:

а) прямая SO перпендикулярна к прямой BD;

б) прямая SO не перпендикулярна к прямой АС;

в) прямая SO не перпендикулярна к плоскости АВС;

г) прямая АС обязательно перпендикулярна к плоскости BDS;

д) если АВ = 6 см; BC = 8 см и AS = 13 см, то SO = 12 cm.

4) Расстояние от точки S до всех вершин прямоугольного треугольника ABC (C = 90°) одинакова, точка О - середина гипотенузы АВ. Укажите, какие из приведенных ниже утверждений правильные, а какие - неправильные:

а) прямая CO не может быть перпендикулярна к плоскости SAB;

б) прямая CO обязательно перпендикулярна к прямой SO;

в) прямая SO обязательно перпендикулярна к плоскости АВС;

г) если АС = 6 см, BC = 8 см и CS = 13 см, то SO = 12 см.