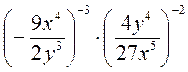Урок № 28
Тема. Стандартный вид числа
Цель: усвоение учащимися содержания алгоритмов выполнения действий умножения и деления чисел, записанных в стандартном виде; формирование умений учащихся применять изученные алгоритмы для выполнения названных действий с числами, записанными в стандартном виде при решении физических и геометрических задач.
Тип урока: усвоение знаний и умений.
Наглядность и оборудование: опорный конспект «Степень с целым отрицательным показателем».
Ход урока
I. Организационный состояние
II. Проверка домашнего задания
Учитель организует работу учащихся с проверки домашнего задания по образцу (с комментарием).
Для «сильных» учеников предлагаем индивидуальные задания на карточках.
III. Формулировка мсти и задач урока
С целью создания соответствующей мотивации учебной деятельности учащихся на уроке можно предложить им к решению какую-нибудь физическую задачу (по изученным на уроках физики материалом), решение которой связано с выполнением действий умножения и деления числовых значений физических величин, записанных в стандартном виде.
Проблемы, которые, возможно, возникнут при решении этой задачи, формулируются в утверждение, которое выражает основную дидактическую цель урока: сформулировать правила выполнения умножения и деления чисел, записанных в стандартном виде, сформировать умения выполнять эти действия за сфомульованими правилам и решать задачи, предусматривающие выполнение умножения и деления чисел, записанных в стандартном виде.
IV. Актуализация опорных знаний и умений
@ С целью успешного восприятия учащимися учебного материала урока перед изучением нового материала следует активизировать знания и умения учащихся: запись чисел в стандартном виде; выполнение умножения и деления десятичных дробей и рациональных чисел (преобразования отношения двух рациональных числовых выражений на рациональное число или десятичная дробь); применение свойств степени с целым показателем; свойства умножения рациональных чисел и их применение (особенно связующее свойство).
Выполнение устных упражнений
1. Какое из чисел записано в стандартном виде?
а) 0,3 ∙ 105; б) 5,8 ∙ 10-3; в) 15 ∙ 10-1; г) 1,00001 ∙ 101.
Для чисел, записанных в стандартном виде, назовите порядок числа.
2. Найдите пропущенное число в стандартном виде числа:
а) 35 = ... ∙ 101; б) 0,027 = ... ∙ 10-2; в) 1035 = ... ∙ 103; г) 0,000285 = ... ∙ 10-5.
3. Выполните действия: a) 10-3 ∙ 105; б) 10-3 : 105; в) (10-5 ∙10-3) : 10-8; г) 4,25 ∙ 0,8; д) 0,25 ∙ 1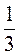 ∙ 40; есть) 8 ∙ 3,7 ∙ 0,125.
∙ 40; есть) 8 ∙ 3,7 ∙ 0,125.
V. Усвоение знаний
План изучения нового материала
1. Умножение чисел, записанных в стандартном виде. Пример.
2. Деление чисел, записанных в стандартном виде. Пример.
@ Бесспорно, учащиеся на момент изучения материала урока уже имеют опыт работы со значениями физических величин, записанных в стандартном виде. Поэтому на уроке учитель имеет только подвести теоретическую базу под правило, что может восприниматься учениками на интуитивном уровне:
1) правило умножения чисел, записанных в стандартном виде, опирается на соединительную свойство умножения;
2) правило деления чисел, записанных в стандартном виде, опирается на представления учащихся о правило умножения рациональных дробей (в обратном порядке).
Эти выводы учащиеся могут сформулировать или во время фронтальной беседы, обсуждая предложенные решения задач на умножение и деление чисел, записанных в стандартном виде, или во время самостоятельной работы (или работы в малых группах) с предложенными в тексте учебника примерами.
Подводя итоги работы по изучению нового материала, обязательно следует подчеркнуть, что во время выполнения названных действий с числами, записанными в стандартном виде, результат них действий должен быть записан в стандартном виде. (Этот момент масс быть запечатлен во время проверки усвоения учащимися материала урока на этапе подведения итогов урока).
VI. Формирование умений
Выполнение устных упражнений
1. Прокомментируйте выполнены действия:
а) (1,5 ∙ 10-3) ∙ (9 ∙ 108) = (1,5 ∙ 9) ∙ (10-3 ∙ 108) = 13,5 ∙ 105 = 1,35 ∙ 106.
б) (2 ∙ 10-3) : (5 ∙ 10-5) = (2 : 5) ∙ (10-3 : 10-5) = 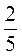 ∙
∙ 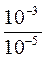 = 0,4 ∙ 102 = 4 ∙ 101.
= 0,4 ∙ 102 = 4 ∙ 101.
2. Выполните действия:
а) 2 ∙ 105 ∙ 5 ∙ 10-5; б) 3 ∙ 10-3 : 6 ∙ 10-3; в) 2,1 ∙ 10-5 ∙ 3 ∙ 10-3; г) 5 ∙ 10-3 : 2 ∙ 10-5.
3. Чему равна площадь прямоугольника со сторонами а = 2,5 ∙103 м и b = 2 ∙ 102 м?
Выполнение письменных упражнений
Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:
1. Умножения (деления) чисел, записанных в стандартном виде.
1) Выполните умножение и запишите результат числом в стандартном виде:
а) (2,3 ∙ 104) ∙ (1,2 ∙ 10-7);
б) (5,1 ∙ 10-5) ∙ (6,8 ∙ 10-7);
в) (4,8 ∙ 10-12) ∙ (1,5 ∙ 105);
г) (5,9 ∙ 1011) ∙ (8,2 ∙ 10-11).
2) Выполните деление и запишите результат числом в стандартном виде:
а) (9,9 ∙ 107) : (1,1 ∙ 10-11);
б) (1,3 ∙ 107) : (6,5 ∙ 10-3);
в) (8,1 ∙ 10-11) : (1,8 ∙ 10-4);
г) (1,1 ∙ 10-5) : (6,4 ∙ 10-13).
3) Выполните умножение:
а) (3,25 ∙ 102) ∙ (1,4 ∙ 103);
б) (4,4 ∙ 10-3) ∙ (5,2 ∙ 104).
4) Выполните деление:
а) (9,9 ∙ 102) : (1,2 ∙ 10-1);
б) (1,23 ∙ 10-3) : (4,8 ∙ 10-2).
2. Прикладные задачи.
1) Известно, что первая космическая скорость равна 7,9 ∙ 103 м/с, вторая -1,12 ∙ 104 м/с, третья - 1,667 ∙ 104 м/с. Выразите эти скорости в километрах в секунду и запишите полученные результаты числами в стандартном виде.
2) Какой путь пройдет свет за 2,8 ∙ 106 с (скорость света равна 3 ∙ 105 км/с)?
3) Масса Земли равна 5,98 ∙ 1024 кг, а масса Марса 6,4 ∙ 1023 кг. Что больше: масса Земли или масса Марса, и во сколько раз? Результат округлите до десятых.
4) Плотность железа 7,8 ∙ 103 км/м3. Найдите массу железной плиты, длина которого 1,2 м, ширина - 6 ∙ 10-1 м и толщина 2,5 ∙ 10-1 м.
3. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.
1) Выполните действия над числами, записанными в стандартном виде:
а) 8,7 ∙ 104 + 5,6 ∙ 104;
б) 3,6 ∙ 103 + 4,71 ∙ 102;
в) 9,3 ∙ 10-3 - 8,4 ∙ 10-3;
г) 2,26 ∙ 105 - 1,3 ∙ 104.
2) Порядок числа х равна 15. Каков порядок числа: а) 1000х; б) 0,0001х; в) 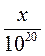 ; г)
; г) 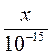 ?
?
3) Порядок числа х равна 7, а порядок числа в - 9. Каким должен быть порядок произведения ху; порядок доли 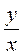 ?
?
4) Вставьте пропущенный выражение:
3 ∙ 1058 |
5 ∙ 1025 |
6∙ 1034 |
63b9c3 |
7bc2 |
? |
4. Упражнения на повторение (запись числа в стандартном виде, выполнение действий со степенями с целым отрицательным показателем, преобразование рациональных выражений, решение рациональных уравнений и т.п.).
1) Найдите значение выражения 1,5х3у2 ∙ 6,2х4у-1, если: а) х = 5,5, y = 0,84; б) x = -0,6, у = -3,2.
2) Упростите выражение: а) 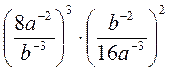 ; б)
; б) 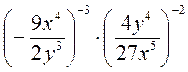 .
.
3) Округлите число до десятков и полученный результат запишите в стандартном виде: а) 1427, б) 155,678; в) 54,23; г) 4911,2.
@ Решая письменные упражнения, ученики должны восстановить оперативные умения по выполнению умножения и деления рациональных чисел (целых чисел, десятичных дробей, обыкновенных дробей) и сформировать навыки применения этих умений во время выполнения умножения и деления чисел, записанных в стандартном виде. Также учащиеся должны сформировать умение применять приобретенные навыки работы с числами, записанными в стандартном виде при решении текстовых (физических и геометрических задач.
Учитывая тот факт, что изучение темы близится к концу, следует уделить внимание решению упражнений на повторение изученного материала (упражнения на применение определения и свойств степени с целым показателем).
VII. Итоги урока
В любом из случаев правильно выполнено действие?
1) (5,2 ∙ 103) ∙ (3 ∙ 10-5) = 15,6 ∙ 10-2;
2) (5,2 ∙ 103) ∙ (3 ∙ 10-5) = 15,6 ∙ 108;
3) (5,2 ∙ 103) ∙ (3 ∙ 10-5) = 1,56 ∙ 10-2;
4) (5,2 ∙ 103) ∙ (3 ∙ 10-5) = 1,56 ∙ 10-1.
VIII. Домашнее задание
1. Изучить правила выполнения умножения и деления чисел, записанных в стандартном виде.
2. Решить задачу на выполнение умножения и деления чисел, записанных в стандартном виде (содержания, аналогичного упражнений классной работы).
3. На повторение: определение функции, области определения и области значения функции, графика функции; решить задачи на вычисление значений функции и построение графика линейной функции.
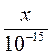 ?
?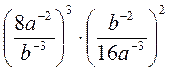 ; б)
; б)