Часть 1 МЕХАНИКА
Глава 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
2.15. Работа. Энергия
Пусть тело, на которое действует сила F, двигаясь по некоторой траектории,
проходит путь s. При этом под действием силы или
меняется скорость тела (сила придает телу ускорение), или компенсируется действие
другой силы (или сил), что противодействует движению. Действие силы F на пути в характеризуют величиной, которую называют
работой.
Работа - это скалярная величина, равная
произведению проекции силы на направление перемещения РS на пути s, который проходит точка приложения силы,

Выражение (2.35) справедлив в том
случае, если проекция силы на направление перемещения остается неизменной. В частности,
это происходит тогда, когда тело движется прямолинейно, а стала за числовым значением
сила 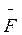 образует с направлением движения постоянный угол α.
образует с направлением движения постоянный угол α.
Поскольку Fs = F cos α, выражение (2.35) можно записать так:

Работа - алгебраическая величина. Если
сила и направление перемещения образуют острый угол (cos α > 0), то работа положительна. Если
угол α тупой (cos α), работа отрицательная. При α
= π/2 работа равна нулю. Следовательно,
понятие работы в механике существенно отличается от обычного представления о
работу.
Если проекция силы на направление
перемещения не остается постоянной во время движения, то для определения работы путь s разделяют на элементарные участки As так, чтобы во время прохождения телом
этого участка силу Fs можно было считать практически
неизменной. Тогда работа на каждом элементарном участке будет

а
работа на всем пути -
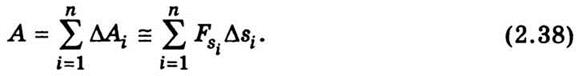
При следовании всех Δsi, к нулю приближенное равенство (2.38)
переходит в точную:
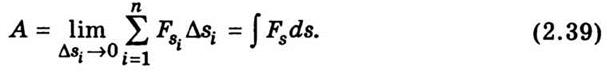
На рис. 2.8 построен график зависимости Fs от положения точки вдоль
траектории (горизонтальную ось можно назвать осью s, а длина отрезка вдоль этой оси между точками s1 и s2
равна длине пути). Из рисунка видно, что работа А на пути от точки 1 до
точки 2 численно равна площади фигуры, ограниченной кривой, ординатами, что
проходят через точки s1 и s2,
и осью s.
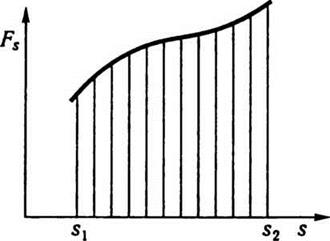
Рис. 2.8
Опыт показывает, что некоторые тела способны
выполнять работу над другими телами. Физическую величину, которая характеризует
способность тела или системы тел совершать работу, называется энергией. Энергия
тела может быть связано, во-первых, движением тела с некоторой скоростью, а во-вторых,
нахождением его в потенциальному поле сил. Энергию первого типа называют
кинетической, энергию второго типа - потенциальной. Следовательно, кинетическая энергия - это
энергия движения, а потенциальная - энергия положения.
Кинетическая энергия материальной точки
т, движущийся со скоростью υ,

Умножив на т числитель и
знаменатель выражения (2.40) и приняв во внимание, что произведение mv равно импульса тела р, выражение для кинетической энергии
запишем так:

Работа, выполняемая над телом,
равна изменению его кинетической энергии 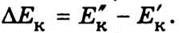
Рассмотрим материальную точку в
потенциальному поле сил. Поставим в соответствие каждой точке поля,
характеризуется радиусом-вектором 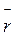 1, определенное значение некоторой функции U(
1, определенное значение некоторой функции U(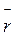 ), осуществив это так. Для некоторой
исходной точки О возьмем произвольное значение функции, равное U0. Чтобы получить значение U1 в некоторой точке 1,
добавим к U0 работу
А10, что выполняется силами поля над телом при его перемещении с
точки 1 в точку 0:
), осуществив это так. Для некоторой
исходной точки О возьмем произвольное значение функции, равное U0. Чтобы получить значение U1 в некоторой точке 1,
добавим к U0 работу
А10, что выполняется силами поля над телом при его перемещении с
точки 1 в точку 0:

Определенная таким образом функция имеет
размерность энергии или работы. Поскольку работа в потенциальному поле сил не
зависит от пути, найденное значение U1 оказывается однозначным.
Аналогично определим значение U(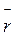 ) для всех точек поля. В частности, значение
U(
) для всех точек поля. В частности, значение
U(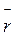 ) в точке 2 будет
) в точке 2 будет

Вычислим разницу U1 - U2. Для этого отнимем от (2.42) выражение (2.43) и
используем тот факт, что A20 = -A02. При этом получим
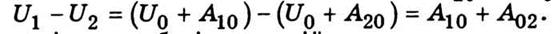
Однако
сумма A10 + A02 равна
работе, которую совершают силы при перемещении тела из точки 1 в точку 2 по
траектории, проходящей через точку О. Однако работа, которая выполняется над телом
при его перемещении по любой другой траектории, будет такой же. Поэтому сумму
A10 + A02 можно
записать как А12, следовательно, получим соотношение

С помощью функции U(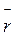 ) можно определить работу, что
осуществляется над телом силами поля на любом пути, ограниченном точками 1 и
2. Эта работа равна уменьшению функции U(
) можно определить работу, что
осуществляется над телом силами поля на любом пути, ограниченном точками 1 и
2. Эта работа равна уменьшению функции U(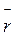 ) на пути 1-2, что дает основание
трактовать физическую величину U(
) на пути 1-2, что дает основание
трактовать физическую величину U(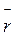 ) как один из разновидностей механической
энергии, которую называют потенциальной.
) как один из разновидностей механической
энергии, которую называют потенциальной.
Каждой точке потенциального поля
соответствует некоторое значение силы F, действующей на тело, и потенциальной
энергии тела U. Следовательно, между силой и потенциальной
энергией должна существовать определенная связь. Для установления этой связи
используем выражение для элементарной работы ΔА
(2.37), которую совершают силы поля при малом перемещении тела Δs, что происходит вдоль произвольно выбранного направления в
пространстве, который обозначим буквой s.
Поскольку в этом случае работа
осуществляется за счет запаса потенциальной энергии, она равна уменьшению
потенциальной энергии на отрезке Δs оси s:

Сравнив (2.37) и (2.45),
достанем 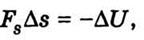

Отсюда имеем среднее значение FS на отрезке Δs. Чтобы получить значение FS в данной точке, надо выполнить
предельный переход

Поскольку U изменяется не только при перемещении вдоль оси s, а и при перемещении вдоль других
направлений, то предел в формуле (2.47)
является производной
от U по оси s:

Для сил, зависящих только от положения
тела, может случиться, что работа, которую они совершают над телом, не зависит от
пути, а определяется лишь начальным и конечным положениями тела в пространстве. В
этом случае поле сил называют потенциальным, а сами силы - консервативными.
Силы, работа которых зависит от пути, по которому тело переходит из одного положения в
другое, называют неконсервативними. Примером неконсервативных сил могут быть
силы трения.
Рассмотрим, как изменяются кинетическая
и потенциальная энергии любой изолированной системы, в которой действуют только
консервативные силы. Элементарная работа консервативных сил равна взятой с
противоположным знаком элементарной изменении потенциальной энергии (2.45). Кроме того,
поскольку другие силы в консервативной системе не действуют, то и самая элементарная
работа равна элементарному изменению кинетической энергии. Следовательно, 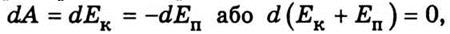 откуда
откуда

Эта
равенство является выражением закона сохранения механической энергии, который утверждает, что
полная механическая энергия консервативной системы не изменяется. Один из основных
законов механики - закон сохранения энергии можно сформулировать так: полная
механическая энергия замкнутой системы тел, между которыми действуют только консервативные
силы, остается постоянной.
В СИ единицей работы является джоуль (Дж),
что равно работе, которую совершает сила в 1 Н на пути в 1 м, а в СГС - эрг, что
равна работе, которую совершает сила в 1 дин на пути в 1 см. Между единицами
существует соотношение:
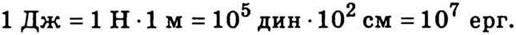
Энергия выражается в тех же
единицах, что и работа.