Часть 1 МЕХАНИКА

Глава 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

2.14. Космические скорости. Освоение космоса

Чтобы тело двигалось вокруг Земли по круговой орбите, которая мало отличается от радиуса Земли R₃, оно должно иметь вполне определенную скорость υ₁. Эту скорость можно определить с равенства 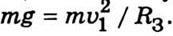Отсюда

Итак, для того чтобы любое тело стало спутником Земли, ему нужно придать скорость υ₁, которую называют первой космической скоростью.

Расстояние спутника от центра Земли r = R₃ + Н, где R₃ - радиус Земли; Н - высота спутника над поверхностью Земли. Поскольку H « R₃, при расчетах величиной Н можно пренебречь. Подставляя значение g и R₃ в формуле (2.29), получим

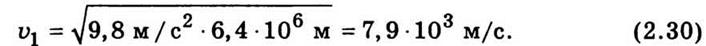
Имея скорость υ₁, тело не будет падать на Землю. Однако этой скорости недостаточно для того, чтобы тело вышло за пределы влияния земного притяжения. Необходимую для этого скорость υ₂ называют второй космической скоростью. Чтобы найти эту скорость, нужно вычислить работу, которая нужна для преодоление силы земного притяжения. Определим эту работу вдоль прямой, проходящей через центр Земли. Элементарная работа на пути dr составит

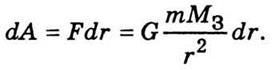
Работу на пути от r = R₃ до r = ∞ определяем интегрированием

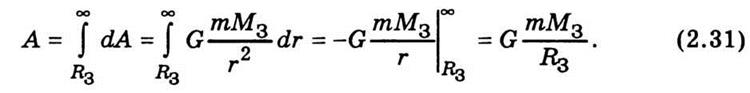
Чтобы преодолеть притяжение Земли и выйти за пределы действия силы земного притяжения, тело должно иметь запас энергии для выполнения работы (2.31). Наименьшая нужна для этого скорость υ₂ и является второй космической скоростью. Ее определим из условия

где 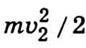- кинетическая энергия тела массой т на поверхности Земли.

Поскольку ускорение свободного падения 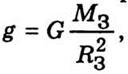то

Сравнивая (2.33) и (2.29), видим, что вторая космическая скорость в 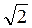раз больше первой. Произведение 7,9 км/с на 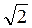дает для υ₂ значение около 11,2 км/с. По этой скорости тело преодолевает силу земного притяжения и движется по параболе; траектория его становится гиперболической, если υ > 11,2 км/с. При υ₃ ≥ 16,7 км/с тело выйдет за пределы Солнечной системы. Эту скорость называют третьей космической скоростью (рис. 2.7).

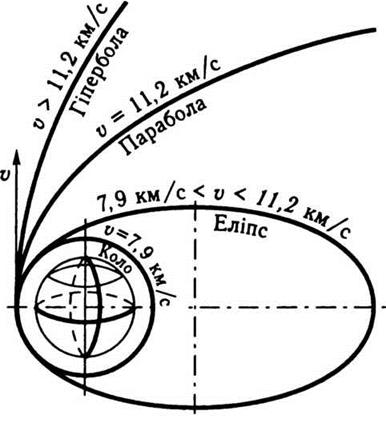
Рис. 2.7.

К. Е. Циолковский вывел формулу для определение скорости полета ракеты. С учетом действия на ракету силы тяжести и сопротивления воздуха скорость ракеты при вертикальном старте можно определить по формуле

где υ_к - конечная скорость при сгорании всего топлива; k - коэффициент, учитывающий сопротивление воздуха и силу тяжести; υ - скорость истечения газов из сопла двигателя; М₀ - начальная масса ракеты; М_к - конечная масса ракеты.

Как видно из формулы (2.34), конечная скорость ракеты υ_к зависит от двух величин - скорости истечения газов и отношение масс полной и пустой ракеты 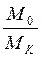. Это отношение называют числом Циолковского и обозначают буквой Z.

Отсюда понятна причина использование многоступенчатых ракет: освобождаясь от балласта, уменьшают массу ракеты и, следовательно, увеличивают ее скорость (число Циолковского увеличивается). К. Е. Циолковский является основоположником теоретической космонавтики.

4 октября 1957 г. старт мощной ракеты с космодрома Байконур положил начало новой эре в научно-техническом прогрессе человечества.

12 апреля 1961 г. в бывшем СССР стартовал космический корабль «Восток», который впервые пилотировавшая человек, летчик-космонавт Ю. О. Гагарин.

Искусственные спутники Земли ежедневно несут трудовую космическую вахту, широко применяются для решения различных научных и практических задач народного хозяйства - метеорологии, дальнего радиосвязи, телевидения, навигации, разведки природных ресурсов нашей планеты и т.д.