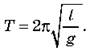ЭЛЕКТРОДИНАМИКА

2-й семестр

Колебания и волны

УРОК 3/25

Тема. Гармонические колебания математического и пружинного маятников

Цель урока: ознакомить учащихся с законами колебаний математического и пружинного маятников.

Тип урока: урок изучения нового материала.

ПЛАН УРОКА

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

1. Математический маятник

Чтобы найти период колебаний груза, подвешенного на нитке, необходимо немножко «идеализировать» задачи. Во-первых, будем считать, что размеры груза намного меньше длины нити, а нить - нерастяжимая и невесомая. Во-вторых, будем считать угол отклонения маятника достаточно малым (не более 10-15°).

Ø Математическим маятником называется идеализированная колебательная система без трения, состоящая из невесомого и нерастяжимого нити, на которой подвешена материальная точка.

Расчеты показывают, что

Ø период колебаний математического маятника равен:

Мы можем убедиться на опытах, что период колебаний математического маятника не зависит от массы груза и определяют его только длиной нити.

Поскольку период колебаний математического маятника зависит от ускорения свободного падения g, то с помощью маятника можно делать точные измерения g.

Известно, что в разных точках земного шара ускорение свободного падения разное. Оно зависит не только от формы Земли, но и от наличия в ее недрах тяжелых (металлы) или легких (газ, нефть) веществ. Итак, получается, что и период колебаний маятника в разных точках будет разный. Это свойство используют, в частности, для определения залежей полезных ископаемых.

Формула периода колебаний математического маятника впервые была установлена голландским ученым Христианом Гюйгенсом. Получив эту формулу, Гюйгенс тем самым доказал, что малые колебания маятника происходят с периодом, не зависит от их амплитуды. Используя это свойство и назвав ее ізохронністю маятника, Гюйгенс в 1657 году сконструировал первые маятниковые часы.

2. Пружинный маятник

Подвешивая к пружине грузы различной массы, можно заметить, что в соответствии с увеличения массы в 4 раза период колебаний увеличивается в 2 раза. А если тот же груз подвешивать к пружин разной жесткости, то можно заметить, что с увеличением жесткости пружины уменьшается период колебаний маятника.

Расчеты показывают, что

Ø период малых колебаний пружинного маятника равен:

Отметим, что как для пружинного, так и для математического маятников период колебаний не зависит от амплитуды. Это важное общее свойство гармонических колебаний. Ее используют, например, в механических часах.

В отличие от маятниковых часов, пружинные часы можно сделать настолько малыми, что их можно носить на руке.

ВОПРОС К УЧАЩИМСЯ В ХОДЕ ИЗЛОЖЕНИЯ НОВОГО МАТЕРИАЛА

Первый уровень

1. Приведите примеры физического, нитяного и пружинного маятников.

2. Как изменится период колебаний математического маятника, если массу груза увеличить (уменьшить)?

3. Назовите причины свободных колебаний математического маятника.

4. Назовите причины свободных колебаний пружинного маятника.

Второй уровень

1. При каком условии колебания математического маятника можно считать гармоническими?

2. Как изменится период колебаний пружинного маятника, если амплитуду колебаний уменьшить в два раза?

3. Что общего в свободных колебаниях математического и пружинного маятников?

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1). Качественные вопросы

1. Когда период колебаний математического маятника больше: зимой или летом?

2. Подвешенный на пружине груз, находясь в равновесии, растягивает пружину на 10 см. Хватит ли этих данных, чтобы найти период колебаний груза на пружине?

3. Как изменился ход маятниковых часов, привезенных из Киева на научную станцию в Антарктиде?

2). Учимся решать задачи

1. Когда к пружине подвесили груз, она растянулась на 20 см. Груз отвели вниз и отпустили. Период Т колебаний, что возникли?

2. Стальной шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить медный шарик того же радиуса? (Ответ: уменьшится в 1,07 раза.)

3. Какое отношение длин двух математических маятников, если один из них делает 31 колебания за то же время, за которое второй выполняет 20 колебаний? (Ответ: длина второго маятника больше в 2,4 раза.)

ЧТО МЫ УЗНАЛИ НА УРОКЕ

· Математическим маятником называется идеализированная колебательная система без трения, состоящую из невесомой и нерастяжимого нити, на которой подвешена материальная точка.

· Период колебаний математического маятника равен:

· Период малых колебаний пружинного маятника равен:

Домашнее задание

1. Подр.: § 19.

2. 3б.:

Рів1 № 10.5; 10.8; 10.20; 10.21.

Рів2 № 10.36; 10.37; 10.38; 10.39.