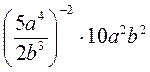Урок № 26
Тема. Свойства степени с целым отрицательным показателем
Цель: закрепить знания учащихся о определение и свойства степени с целым (отрицательным) показателем и сформировать умение использовать их для решения упражнений на вычисление значений числовых выражений и преобразования выражений с переменными.
Тип урока: отработка навыков, диагностика усвоения.
Наглядность и оборудование: опорный конспект «Степень с целым отрицательным показателем».
Ход урока
I. Организационный состояние
II. Проверка домашнего задания
Для того чтобы разнообразить работу учащихся, проводим игровой момент «Найди ошибку» (за упражнениями домашней работы).
Для «сильных» учеников предлагаем индивидуальные задания на карточках.
III. Формулировка мсти и задач урока
Проведена проверка выполнения домашнего задания и анализ возможных ошибок сами по себе создают мотивацию учащихся к деятельности по устранению причины ошибок (коррекции знаний), а также совершенствования умений. Поэтому именно коррекция знаний учащихся относительно содержания определения и свойств степени с целым показателем и отработки умений учащихся выполнять преобразование рациональных выражений, содержащих степени с целыми показателями, с использованием изученных алгоритмов выполнения преобразований и составляют основную дидактическую цель урока.
IV. Актуализация опорных знаний и умений
@ С целью успешного восприятия учащимися учебного материала урока перед изучением нового материала следует активизировать знания и умения учащихся: определение и свойства степени с целым показателем и способ применения для вычисления значений числовых выражений, содержащих степени с целым показателем, а также для преобразования рациональных выражений, содержащих степени с целым показателем.
Выполнение устных упражнений
1. Представьте выражения в виде одночлена: t2 ∙ t5; (т3)2; 7 : а; (ху)5.
2. Упростите выражения: t -3 ∙ t 6; 3 : а -2; (а -6) -2; (а -5b -2) -3.
3. Вычислите значение выражений удобным способом: 2 -13 ∙ 2 25 : 2 12 ; (5 -5) -13 : (5 -16) -4; 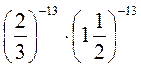 .
.
V. Отработка умений
Выполнение письменных упражнений
@ С целью формирования устойчивых умений, которые впоследствии превратятся в устойчивые навыки применения свойств степени с натуральным показателем, упражнения для письменного решения должны быть составлены так, чтобы каждая требовала от учащихся применения всех 5-ти свойств степени. Формулировка самих заданий может повторять содержание заданий предыдущего урока (конечно, на более высоком уровне сложности).
Основное внимание на уроке уделяется формированию устойчивых умений преобразовывать выражения с применением изученных свойств степени. При этом учитель может подчеркнуть, что в результате выполненных действий в ответе можно получить степень с целым отрицательным показателем, при этом, если иначе не сказано в условии, не обязательно переходить к выражений со степенями с натуральным показателем. Также следует напомнить о том, что, преобразуя выражения, содержащие степени, основы которых - числа, ученики должны стараться подать компоненты выражений в виде степеней с одинаковыми основаниями.
Для реализации дидактической цели на этом уроке следует решить задачи следующего содержания:
1. Вычисление значений числовых выражений (предварительно применив соответствующее свойство степени).
1) Вычислите:
а) 16-1 ∙ 25 ∙ 42; б) 58 : (125 : 25-1); в) (93 : 3-5) : 27-2; г) 4-5 ∙ 33 ∙ 0,25-5; д) 2-8 ∙ 1,25-8 ∙ 0,4-8; е) 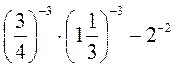 .
.
2) Вычислите: а) 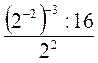 ; б)
; б) 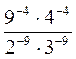 ; в)
; в) 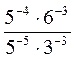 .
.
3) Вычислите: а) 8 -2 ∙ 43; б) 9 -6 ∙ 275; в) 100 : 10 -3; г) 125 -4 : 25 -5; д) 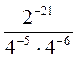 ; е)
; е) 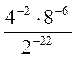 ; ж)
; ж) 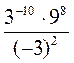 ; з)
; з) 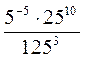 .
.
2. Представление выражения в виде степени с поданной основой (степени или имеют одинаковую основу или требуют перехода к одной основы).
1) Представьте выражение в виде степени с основанием 3 и найдите его значение:
а) 27 ∙ 3 -4; б) (3-1)5 ∙ 812; в) 9 -2 : 3-6; г) 813 : (9 -2) -3.
2) Представьте в виде степени с основанием 5 выражение, в котором m - целое:
а) 5m ∙ 5m+1 ∙ 51-m; б) (5m)2 ∙ (5-3)m; в) 625 : 54m - 2.
3. Упрощение выражений.
1) Упростите выражение:
а) (а -1 - 1)(a -1 + 1) - а -2; б) (b -3 - 3)(b -3 + 3) - b-3(b-3 + 2); в) (x -1 - -2)2 - (x -1 + y -3)2; г) (с-1 - с)2 - (с-1 - 2с2)(с-1 +2с2); д) (a-1 - b-1)(-2 + а-1b-1 + b-2); с) 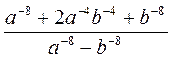 .
.
2) Упростите выражение:
а) 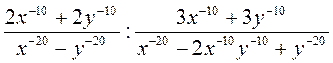 ; б)
; б) 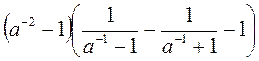 ; в)
; в) 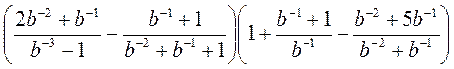 .
.
3) Упростите выражение:
а) 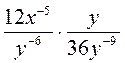 ; б)
; б) 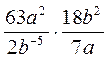 ; в)
; в) 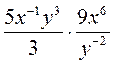 ; г)
; г) 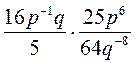 .
.
4) Упростите выражение: а) 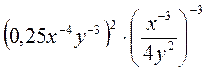 ; б)
; б) 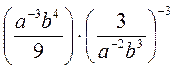 ; в)
; в) 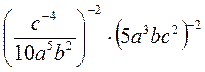 ; г)
; г) 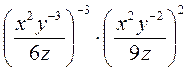 .
.
4. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний.
1) Упростите выражение: а) 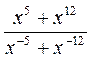 ; б)
; б) 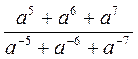 .
.
2) Докажите, что при любом целом п равенство является правильной: а) 2n + 2n = 2п+1; б) 2∙3n + 3n = 3n+1.
3) Найдите пропущенный выражение:
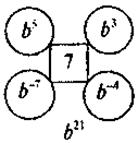
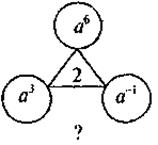
5. На повторение упражнения, предусматривающие преобразование рациональных выражений.
1) Упростите выражение:
а) 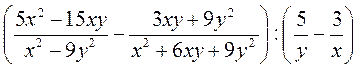 ;
;
б) 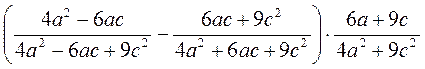 .
.
VI. Итоги урока
Самостоятельная работа № 6
Вариант 1 |
Вариант 2 |
1. Выполните действия: |
|
а) 5-1 - 3 ∙ 2-3; б) 2-10 ∙ 26; в) (x - 7)-2; г) 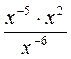 . . |
а) 6-1 - 2∙3-2; б) 512 ∙ 5-8; в) а-3 : а-6; г) (а-4)3 ∙ а10 |
2. Упростите выражение: |
|
a) 1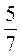 x6в -10 ∙ 0,7x-4у2; г) x6в -10 ∙ 0,7x-4у2; г) 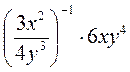 . . |
а) 1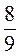 а7b-12 ∙ 0,9a-5b13; б) а7b-12 ∙ 0,9a-5b13; б) 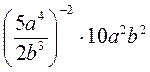 . . |
3. Вычислите: |
|
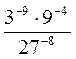
|
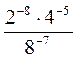
|
VII. Домашнее задание
1. Повторить содержание определения и свойств степени с целым отрицательным показателем.
2. Выполнить упражнения другого варианта самостоятельной работы (провести анализ ошибок за розданными разрешениями).
3. Повторить правила выполнения умножения и деления числа на разрядную единицу (справочник, 5 класс).
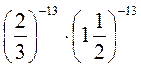
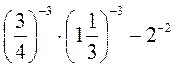 .
.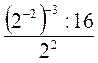 ; б)
; б) 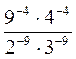 ; в)
; в) 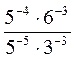 .
.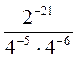 ; е)
; е) 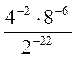 ; ж)
; ж) 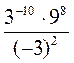 ; з)
; з) 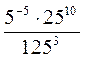 .
.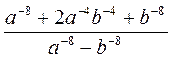
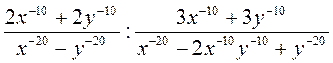
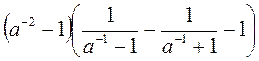 ; в)
; в) 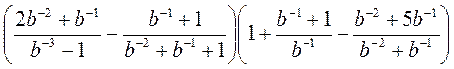
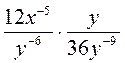 ; б)
; б) 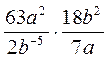 ; в)
; в) 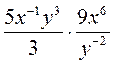 ; г)
; г) 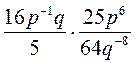
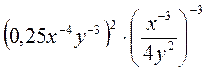 ; б)
; б) 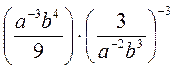 ; в)
; в) 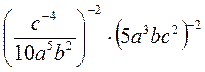 ; г)
; г) 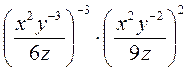
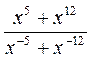 ; б)
; б) 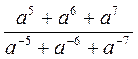 .
. 

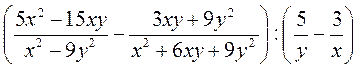 ;
;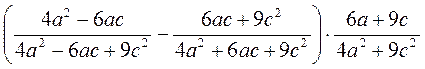 .
.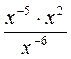 .
.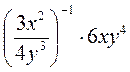 .
.