Урок № 25

Тема. Свойство медианы, биссектрисы и высоты равнобедренного треугольника

Цель: добиться сознательного восприятие учащимися содержания теоремы о свойстве медианы, биссектрисы и высоты равнобедренного треугольника и следствий из нее; сформировать умение воспроизводить названные свойства и применять их при решении задач.

Тип урока: усвоение знаний, умений и навыков.

Наглядность и оборудование: набор демонстрационного чертежных принадлежностей; таблица; раздаточный материал.

ХОД УРОКА

I. Организационный момент

II. Проверка домашнего задания

Домашнее задание проверяем у учащихся, требующих дополнительного педагогического внимания.

III. Актуализация опорных знаний

Практическая работа по готовыми рисунками

1. Проверьте, является ли треугольник равнобедренным. Если да, назовите и запишите его основу, боковые стороны.

2. С вершины, противоположной основы, проведите последовательно:

а) медиану;

б) бісектрису;

в) высоту.

Что вы заметили? Сформулируйте гипотезу.

3*. Из вершин при основании проведите:

а) медианы, сравните их длины;

б) биссектрисы, сравните их длины;

в) высоты, сравните их длины.

Что вы заметили? Сформулируйте гипотезу.

Методика проведения практической работы

Каждый ученик (или малая группа - на усмотрение учителя) получает лист с изображением равнобедренного треугольника и последовательно выполняет задания практической работы. После выполнения работы группы презентуют свои гипотезы, происходит осмысленное целеполагание урока (учитель может собрать листы и оценить умение учащихся выполнять построения медиан, биссектрис и высот треугольника.)

V. Усвоение новых знаний

План изучения нового материала

1°. Формулировка теоремы о медиану, бісектрису, высоту равнобедренного треугольника.

2°. Следствие из теоремы.

3°. Применение теоремы:

а) для доведения того, что треугольник равнобедренный [метод удвоения медианы];

б) для выполнения изображение равнобедренного треугольника.

Метод удвоения медианы не является обязательным для рассматривания, но можно его изучить в классах с высоким уровню подготовки учащихся и желательно подкрепить задачним материалом.

Также важным является вопрос о практическом применении теоремы о медиану, бісектрису, высоту равнобедренного треугольника, а именно: как построить равнобедренный треугольник на практике?

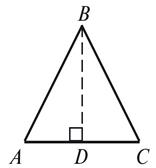
1. Строим произвольный отрезок, AC - основа.

2. Делим отрезок AC пополам, D - середина AC.

3. Через точку D проведем перпендикуляр к AC. На прямой обозначим точку B.

4. Δ ABC - искомый равнобедренный.

VI. Первичное осознание нового материала

Выполнение устных упражнений

1. В треугольнике ABC отрезок AD - медиана, биссектриса и высота. Назовите равные стороны треугольника.

2. В треугольнике 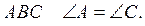Биссектриса которого из углов треугольника совпадает с медианой и высотой?

3. В рівнобедреному, но не равностороннем треугольнике проведены все медианы, биссектрисы и высоты. Сколько различных отрезков проведен? Как изменится ответ, если данный треугольник является равносторонним?

4. В треугольнике 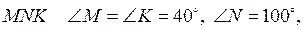NP - медиана. Найдите углы ΔMNP.

5. Как в рівнобедреному треугольнике OMK с основой OK провести высоту (бісектрису) из вершины M, используя только линейку с делениями?

Выполнение письменных упражнений

1. Начертите равнобедренный треугольник ABC с основанием AC и тупым углом B.

а) Проведите высоту AD. Лежит ли точка D на отрезке BC?

б) Проведите медиана BM. Или равны углы ABM и CBM? Почему?

2. В треугольнике 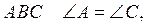BD - биссектриса треугольника. Докажите, что AD = CD.

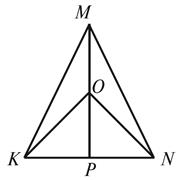
3. На высоте равнобедренного MP треугольника KMN с основой KN обозначено точку O (рис. 1). Докажите, что треугольник KON равнобедренный.

4. Докажите, что медианы равных треугольников, проведенные к соответственно равным сторонам, равны.

5. Треугольники ABC и DBC уровне (рис. 2). Докажите, что точка пересечения отрезков AD и BC делит отрезок AD пополам.

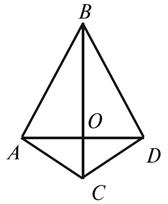
Підчасрозв'язуваннязадачслідвимагативідучнівзастосуваннясформульованих на уроке утверждений для аргументации своих рассуждений как можно чаще. Также желательно продолжать начатую на предыдущих уроках работу по формированию умений рассуждать «от конца до начала» (там, где это уместно - в задачах достаточного и высокого уровня).

VII. Итоги урока

Или правильное утверждение: «Медиана равнобедренного треугольника совпадает с высотой и биссектрисой»?

VIII. Домашнее задача

Устно выполнить упражнение.

Может ли медиана треугольника совпадать с его высотой, но не совпадать с биссектрисой, проведенной с той самой вершины?

Письменно решить задачи.

1. В треугольнике ABC отрезок CD является медианой и высотой. Докажите,что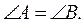

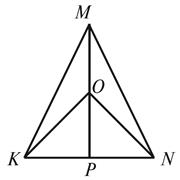
2. В рівнобедреному треугольнике KON с основой KN на продолжении биссектрисы OP обозначено точку M (рис. 3). Докажите, что треугольник KMN равнобедренный.

3. Перпендикулярные отрезки AD и BC пересекаются в точке O, причем 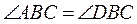(рис. 4). Докажите, что треугольник ACD равнобедренный.

Источники:

1. Уроки геометрии. 7 класс./ С. П. Бабенко - Х.: Изд. группа «Основа», 2007.- 208 с.