Урок № 24

Тема. Медиана, биссектриса и высота треугольника

Цель: добиться усвоения учениками:

· содержания понятий «медиана треугольника»; «биссектриса треугольника»; «высота треугольника»;

· представление о положении высот в различных видах треугольника.

Сформировать умения:

· изображать медианы, высоты и биссектрисы треугольника;

· различать эти отрезки, исходя из условия задачи.

Тип урока: применение знаний, умений и навыков.

Наглядность и оборудования: набор демонстрационного чертежных принадлежностей; таблица «Медиана, высота, биссектриса треугольника».

Таблица

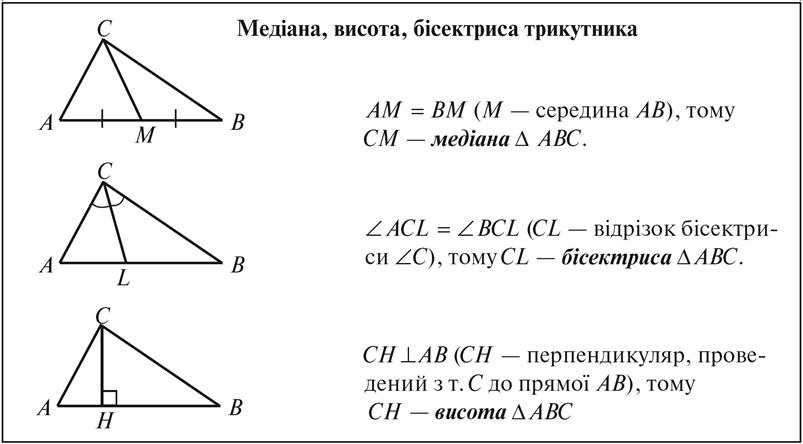
ХОД УРОКА

I. Организационный момент

II. Проверка домашнего задания

Самостоятельная работа

Вариант 1

1. Основа равнобедренного треугольника в 2 раза меньше его боковой стороны, а периметр равна 15 см. Найдите стороны треугольника.

2. В треугольнике ABC (рис. 1) AE = DE; 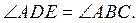Докажите, что Δ ABC - равнобедренный.

Вариант 2

1. Периметр равнобедренного треугольника равен 14 см, а его боковая сторона в 3 раза больше за основу. Найдите стороны треугольника.

2. В треугольнике ABC (рис. 2) AB = BC; 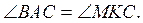Докажите, что ΔKMC - равнобедренный.

Ответы:

Вариант 1. 1. Основа 3 см; боковые стороны по 6 см.

Вариант 2. 1. Основа 2 см; боковые стороны по 6 см.

III. Мотивация учебной деятельности. Формулировка цели и задач урока

На этом этапе изучение геометрии единственно возможным вариантом мотивации могут быть слова учителя о существовании некоторых других (кроме сторон и углов) элементов треугольника и важность их свойств для решения задач.

Исходя из сказанного учителем, основную цель формулируем как изучение определений и формирования умений использовать определение новых элементов для распознавания и построения «новых» элементов треугольника.

IV. Актуализация опорных знаний

Выполнение устных упражнений

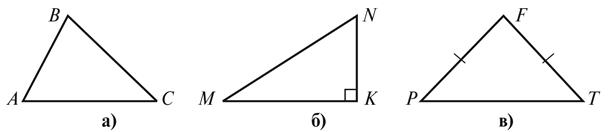
На рисунке 3:

а) назовите элементы каждого из треугольников;

б) определите вид треугольников по сторонам;

в) укажите наибольший угол в каждом треугольнике, определите его вид.

Как теперь можно назвать каждый из треугольников?

V. Усвоение новых знаний

План изучения нового материала

1°. Определение медианы треугольника. Свойства медиан.

2°. Определение биссектрисы треугольника. Свойства биссектрис.

3°. Определение высоты треугольника. Свойства высот.

4°. Положение высоты в различных видах треугольников.

5°. Взаимное расположение высоты, медианы и биссектрисы, проведенных из одной вершины треугольника.

VI. Первичное осознание нового материала

Выполнение устных упражнений

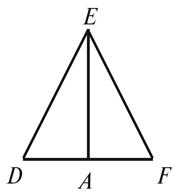
1. В треугольнике DEF проведено отрезок EA (рис. 4). Определите, является ли этот отрезок медианой, биссектрисой или высотой данного треугольника, если:

а) DA = FA;

б)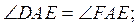

в)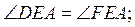

г) DE = FE и DA = FA.

2. Может лежать внутри треугольника только одна из трех его высот; только две из трех его высот?

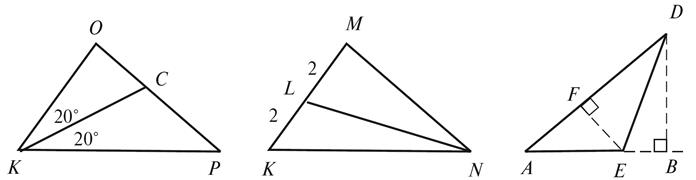
3. Назовите, чем являются отрезки KC,NL, EF и DB для изображенных на рисунке 5 треугольников KOP, MNK и ADE.

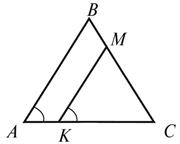
4. В треугольнике ABC проведена бісектрису BK и медиану BM. Известно, что AC = 8 см. Найдите длину отрезка AM и градусную меру угла ABK.

Выполнение графических упражнений

1. Начертите три треугольника - остроугольный, тупоугольный и прямоугольный. Используя угольник, проведите в каждом из них высоту из вершины острого угла.

2. Начертите произвольный треугольник. Сколько медиан можно в нем провести? Постройте их, используя линейку с делениями.

Выполнение письменных упражнений

Уровень А

1. В рівнобедреному треугольнике ABC отрезок BD-медиана, проведенная к основанию. Найдите периметр треугольника ABC, если P_{Δ ABD} =12 см, BD = 4 см.

2. В треугольнике BD - биссектриса треугольника. Докажите, что AD = CD.

Уровень Б

Докажите, что в рівнобедреному треугольнике медианы, проведенные к боковым сторонам, равны.

Уровень В

Докажите равенство треугольников за стороной, прилегающим углом и биссектрисой, проведенной из вершины этого угла.

Письменную задачу 2 можно решить уже на этом уроке как пропедевтическую для теоремы о свойство медианы равнобедренного треугольника, проведенная к основанию, а затем решить ее на следующем уроке после ознакомления учащихся с теоремой и сравнить решение задачи с доведением теоремы.

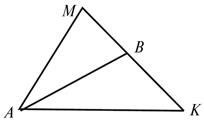
VII. Итоги урока

Сделайте необходимые отметки на рисунке, чтобы отрезок AB был изображением:

а) медианы;

б) высоты;

в) биссектрисы треугольника.

VIII. Домашнее задание

1. Начертите нерівнобедрений треугольник ABC.

а) Отметьте точку M -середину стороны BC. Проведите отрезок AM. Как он называется?

б) Проведите бісектрису угла B и отметьте точку L пересечения со стороной AC. Как называется отрезок BL?

в) Проведите с точки C перпендикуляр CH к прямой AB. Как называется построен отрезок в треугольнике ABC?

2. В рівнобедреному треугольнике ABC отрезок BD-медиана, проведенная к основанию. Найдите периметр треугольника BDC, если P_{Δ ABC} = 18 см, BD = 5 см.

Источники:

1. Уроки геометрии. 7 класс./ С. П. Бабенко - Х.: Изд. группа «Основа», 2007.- 208 с.