УРОК 25
Тема. Решение однородных тригонометрических уравнений
Цель урока: формирование умений учащихся решать однородные тригонометрические уравнения.
И. Проверка домашнего задания
1. Обсуждение решение упражнения № 2 (6; 9; 11) за готовыми решениями.
2. Решения аналогичных упражнений.
а) 1 + cos x + cos 2x = 0;
б) cos4 x - sin4 x = 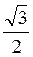 ;
;
в) cos 4x + sin 2x = 0;
г) cos x (tg x - 1) = 0.
Ответы: а)  + πn, ±
+ πn, ± 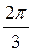 + 2 πn, n
+ 2 πn, n Z; б) ±
Z; б) ± 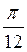 + πn, n
+ πn, n Z;
Z;
в) (-1)n+1 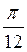 +
+ 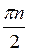 ;
;  + πn, n
+ πn, n Z; г)
Z; г)  + πn, n
+ πn, n Z.
Z.
II. Восприятие и осознание нового материала
1) Рассмотрим уравнение вида asin x + bcos x = 0 (однородное уравнение 1-й степени), где а и b не равны нулю. Значения x, при которых cos x равна нулю, не удовлетворяет данному уравнению, ибо тогда и sin x тоже равнялся бы нулю, а cos x и sin x не могут одновременно равняться нулю. Поэтому можно разделить обе части уравнения почленно на cos x. Имеем:
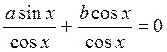 ; atg x + b = 0; tg x = -
; atg x + b = 0; tg x = -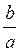 .
.
x = - arctg 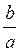 + πn, n
+ πn, n Z.
Z.
Выполнение упражнений
Решите уравнение.
1. а)  sinx + cosx = 0;
sinx + cosx = 0;
б) 16sin x = 5cos x;
в) 2cos 2x + 3sin 2x = 0;
г) sin2 x + sin x cos x = 0.
Ответ: а) - +πn, n
+πn, n Z; б) arctg
Z; б) arctg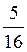 + πn, n
+ πn, n Z; в) -
Z; в) -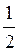 arctg
arctg +
+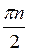 , n
, n Z; г) πn, -
Z; г) πn, - + πn, n
+ πn, n Z.
Z.
2. Уравнения вида a sin2x + b sinx cosx + c cos2x = 0 называется однородным уравнением 2-й степени. Если числа а, b, с не равны нулю, то разделим данное уравнение на cos2 x (или на sin2x). (В данном уравнении cos2x ≠ 0, ибо в противном случае sin2 x тоже равнялся бы нулю, а cos x и sin x не могут одновременно равняться нулю). Тогда
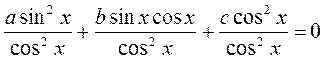 ;
;
atg2x + btgx + c = 0.
Решив полученное уравнение получим корни данного уравнения.
Выполнение упражнений
1. Решите уравнение:
а) sin2 x = 3cos2 x;
б) sin2 x - 3 sin x cos x + 2 cos2 x = 0;
в) 3sin2 x - 4sin x cos x +cos2 x = 0;
г) sin2 x - 5sin x cos x + 6cos2 x = 0.
Ответ: а) ±  + πn, n
+ πn, n Z; б) arctg 2 + πn,
Z; б) arctg 2 + πn,  + πn, n
+ πn, n Z; в)
Z; в)  + πn, arctg
+ πn, arctg 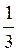 + πn, n
+ πn, n Z; г) arctg 2 + πn, arctg 3 + πn, n
Z; г) arctg 2 + πn, arctg 3 + πn, n Z.
Z.
3. Уравнения вида аn sinn x + an-1 sinn-1x cos x +... + a1 sinx cosn-1x + a0 cosn x = 0
называется однородным уравнением n-ой степени относительно синуса и косинуса.
Если ни один из коэффициентов an, а n-1, ... , a1, a0 не равен нулю, то, разделив обе части уравнения почленно на cosnx, получим уравнение n-ой степени относительно tgx. Если хотя бы один из коэффициентов an, а n-1, ... , a1, a0 равна нулю, то прежде чем выполнять деление на cosnx, следует доказать, что cosnx ≠ 0, т.е. cos x ≠ 0.
Рассмотрим пример:
Решите уравнение cos2 x - 2 cos x sin x = 0.
Делить обе части на cos2 x , cos2 x = 0 является решением данного уравнения. Это уравнение можно решить:
И способ (вынесение множителя)
cos2 x - 2 cos x sin x = 0
cos x (cos x - 2 sin x) = 0
Отсюда cosx = 0 или cosx - 2sinx = 0.
1) cos x = 0; x =  + πn, n
+ πn, n Z.
Z.
2) cosx - 2sinx = 0; 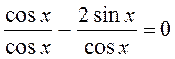 ; 1 - 2tgx = 0; tgx =
; 1 - 2tgx = 0; tgx = 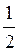 ; x = arctg
; x = arctg 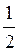 + πn, n
+ πn, n Z.
Z.
Ответ:  + πn, n
+ πn, n Z; arctg
Z; arctg 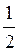 + πn, n
+ πn, n Z.
Z.
II способ. Разделим обе части на sin2 x, поскольку sin x ≠ 0 в данном уравнении, ибо в противном случае и cos x = 0, что невозможно.
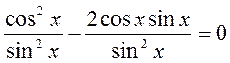 ,
,
ctg2 x - 2ctg x = 0;
ctgх(ctg x - 2) = 0.
Отсюда ctg x = 0, или ctg x = 2.
1) ctg x = 0; x =  + πn, n
+ πn, n Z.
Z.
2) ctg x = 2; x = arcctg 2 + πn, n Z.
Z.
Ответ:  + πn, arcctg 2 + πn, n
+ πn, arcctg 2 + πn, n Z.
Z.
Выполнение упражнений
1. Решите уравнение:
а) sin 2х - cos2 x = 0;
б) 2 sin2 x =  sin 2x;
sin 2x;
в) 3 sin 2x + cos 2x = cos2 x;
г) 1 - cos x = 2 sin 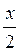 cos
cos 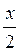 .
.
Ответ: a)  + πn, arctg
+ πn, arctg 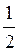 + πn, n
+ πn, n Z; б) πn,
Z; б) πn,  + πn, n
+ πn, n Z; в) πn, arctg 6 + πn, n
Z; в) πn, arctg 6 + πn, n Z; г) 2πn,
Z; г) 2πn,  + 2πn, n
+ 2πn, n Z.
Z.
2. Решите уравнение:
а) 4sin2 x - sin2x = 3;
б) sin 2х + 4cos2 x = 1;
в) 5 sin2 x + 3 sin x cos x - 4 = 0;
г) 2 sin x + cos x = 2.
Ответ: а) arctg 3 + πn, -  + πn, n
+ πn, n Z; б) arctg3 + πn, -
Z; б) arctg3 + πn, -  + πn, n
+ πn, n Z; в) - arctg 4 + πn,
Z; в) - arctg 4 + πn,  + πn, n
+ πn, n Z; г)
Z; г)  + 2πn, 2arctg
+ 2πn, 2arctg 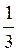 + 2 πn, n
+ 2 πn, n Z.
Z.
III. Подведение итогов урока
IV. Домашнее задание
Раздел II § 3 (3). Вопросы и задания для повторения раздела II № 17, 18. Упражнение№ 2 (8; 17; 22; 28; 36).