УРОК 24
Тема. Решения тригонометрических уравнений способом разложения на множители
Цель урока: фрмування умений учащихся решать тригонометрические уравнения способом разложения на множители.
И. Проверка домашнего задания
Первый ученик объясняет решение упражнения № 2 (23), второй ученик - упражнения № 2 (30), третий - упражнения № 2 (37).
II. Восприятие и осознание нового материала
Много тригонометрических уравнений, правая часть которых равна 0, решаемые разложением их левой части на множители.
Рассмотрим примеры.
Пример 1. Решите уравнение 1 + cos x - 2 cos 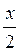 = 0.
= 0.
Решение
Учтя, что 1 + cos x = 2 cos 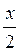 , получим:
, получим:
2cos2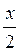 - 2cos
- 2cos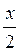 = 0, 2cos
= 0, 2cos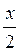
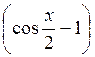 = 0.
= 0.
Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому:
1) cos 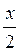 = 0;
= 0; 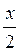 =
=  +πn, n
+πn, n  Z; x = π + 2 πn, n
Z; x = π + 2 πn, n Z;
Z;
2) cos 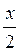 = 1;
= 1; 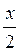 = 2πn, п
= 2πn, п  Z; х = 4 πn, n
Z; х = 4 πn, n Z.
Z.
Ответ: n + 2πn, 4 πn, n Z.
Z.
Пример 2. Решите уравнение sin 2х - sin х = 0.
Решение
sin 2x - sin х = 0; 2 sin 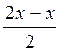 cos
cos 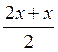 = 0; 2 sin
= 0; 2 sin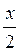 cos
cos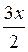 = 0.
= 0.
1) sin 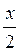 = 0;
= 0; 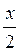 = πn, x = 2 πn, n
= πn, x = 2 πn, n Z.
Z.
2) cos 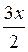 = 0,
= 0, 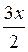 =
=  +πn, x =
+πn, x =  +
+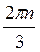 , n
, n Z.
Z.
Ответ: 2πn и  +
+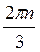 , n
, n Z.
Z.
III. Формирование умений и навыков учащихся решать тригонометрические уравнения способом разложения на множители
Выполнение упражнений______________________________
Решите уравнение.
1. a)  cos х = sin2 х cos х;
cos х = sin2 х cos х;
6) 2sin 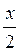 = 3sin2
= 3sin2 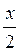 ;
;
в) sin 2x = 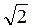 sin x;
sin x;
г) 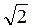 cos2 4x + cos 4x = 0.
cos2 4x + cos 4x = 0.
Ответ: а)  +πn, n
+πn, n Z; б) 2πn, (-1)n2arcsin
Z; б) 2πn, (-1)n2arcsin + 2 πn, n
+ 2 πn, n Z; в) πn, ±
Z; в) πn, ±  + 2 πn, n
+ 2 πn, n Z; г)
Z; г) 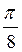 +
+ 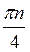 , ±
, ± 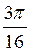 +
+ 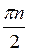 , n
, n Z.
Z.
2. a) cos 7x + cos х = 0;
б) sin 7x = sin х;
в) cos 3x + sin 5x = 0;
г) sin 7x + sin 3х = 3cos 2х.
Ответы: а) 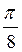 +
+ 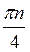 ,
,  +
+ 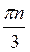 , n
, n Z; б)
Z; б) 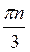 ,
, 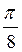 +
+ 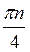 , n
, n Z; в)
Z; в) 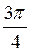 +πn,
+πn, 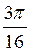 +
+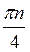 , n
, n Z; г)
Z; г)  +
+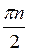 , n
, n Z.
Z.
IV. Подведение итогов урока
V. Домашнее задание
Раздел II § 3 (2). Вопросы и задания для повторения раздела II № 16. Упражнение№ 2 (5; 6; 9; 11).