АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел III. ФУНКЦИЯ

§3. ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ФУНКЦИИ.

Область определения функции у = f(х) будем называть симметричной относительно нуля, если вместе с каждым числом х область определения содержит также и число (-х). Среди функций с областью определение, симметричной относительно нуля, различают четные и нечетные.

Функцию у = f(x) называют парной, если ее область определения симметрична относительно нуля и для каждого х из области определения выполняется равенство f(-х) = f(х).

Пример 1. Исследовать на четность функцию f(x) = х⁴.

Решения. D(f) = (-∞;+∞). Область определения симметрична относительно нуля. Поскольку f(_x) = (-х)⁴ = х⁴ = f(х), то функция четная.

Полезной может быть свойство четной функции: график любой четной функции симметричен относительно оси у.

Функцию у = f(х) называют нечетной, если ее область определения симметрична относительно нуля и для каждого х из области определения выполняется равенство f(-x) = -f(x).

Пример 2. Исследовать на четность функцию f(x) = 10/-x.

Решения. 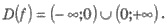Область определения симметрична относительно нуля. Поскольку f(-x) = 10/-x = -f(x), то функция нечетная.

Полезным является свойство нечетной функции: график любой нечетной функции симметричен относительно начала координат.

Пример 3. Исследовать на четность функцию f(x) = 1/(x-2).

Решения. 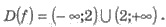Область определения не симметрична относительно нуля, поскольку значение х = -2 принадлежит области определения, а значение х = 2 - не принадлежит. Поэтому функция ни четная, ни не парная.

Пример 4. Исследовать на четность функцию f(х) = х² - х.

Решения. D(f) = (-∞;+∞). Область определения симметрична относительно нуля. Вычислите 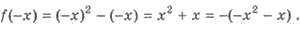Вычислите f(-х) ≠ f(х) и f(-х) ≠ -f(x), то функция ни четная, ни не четная.