АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел III. ФУНКЦИЯ
§1. ОСНОВНЫЕ СВЕДЕНИЯ О ФУНКЦИИ.
7. Промежутки возрастания и убывания функции. Точки максимума и точки минимума функции. Максимумы и минимумы функции.
Функцию у = f(х) называют возрастающей на некотором промежутке, если
большему значению аргумента из этого промежутка соответствует большее значение
функции.
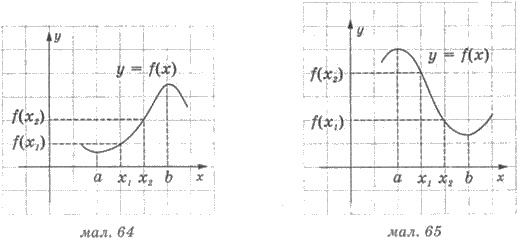
На рисунке 64 изображен график
функции у = f(x), что возрастает на промежутке [а; b] (промежуток [а; b] при этом называют промежутком возрастания функции). Для
любых x1 и x2 из этого промежутка, таких , что х2 > х1 выполняется неравенство f(x2) >
f(x1).
Функцию у = f(x) называют убывающей на некотором промежутке, если большему
значению аргумента из этого промежутка соответствует меньшее значение функции.
На рисунке 65 показан график
функции у = f(x) убывает на промежутке [а; b] (промежуток [а; b] при этом называют промежутком
убывания функции).
Для любых x1 и x2 из этого промежутка, таких, что х2
> х1, выполняется неравенство f(х2)
f(x1).
Пример 1. Для функции у = f(x), заданной графически на рисунке 63 промежутки возрастания:
[-4; -2] и [1; 5], промежутки убывания: [-2; 1] и [5; 6].
Точку х0 называют точкой
максимума функции у = f(x), если для оси х из некоторой окрестности точки х0
выполняется неравенство f(х0) > f(x). Значение функции в точке максимума называют
максимумом функции. На рисунке 64 х = b
- точка максимума
функции, а на рисунке 65 х = а - точка минимума функции. Точку х0
называют точкой минимума функции у = f(x), если для всех х из некоторой окрестности точки х0
выполняется неравенство f(х0) /(х). Значение функции в точке минимума называют минимумом
функции. На рисунке 64 х = а - точка минимума функции, а на
рисунке 65 х = b - точка максимума функции.
Пример 2. Для функции у = f(x) (рис. 63), что задана графически на промежутке [-4; 6]: х =
1 - точка минимума, это записывают так хmin = 1; min = х(1) =
-2 - минимум функции. В
функции две точки максимума х = -2 и х = 5. Это записывают хmax = -2, хmax = 5, уmax = (-2) = 3, max = y(5) = 2 - максимум функции.