УРОК № 24

Тема. Расстояние между двумя точками с заданными координатами

Цель урока: вывод формулы для нахождения расстояния между двумя точками, заданными координатами, и применение формул к решению задач.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Декартовы координаты и векторы на плоскости» [13].

Требования к уровню подготовки учащихся: записывают и доказывают формулу для нахождения расстояния между двумя точками, применяют изученную формулу к решению задач.

Ход урока

И. Проверка домашнего задания, актуализация опорных знаний

1. 1. Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учащихся при выполнении домашних заданий.
2. 2. Математический диктант

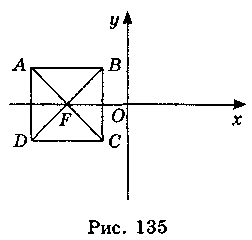
Сторона квадрата (см. рисунок) равна 5.

Вариант 1

Вариант 2

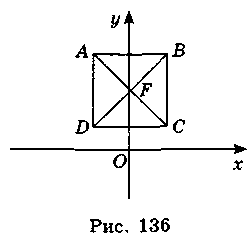
Запишите координаты точек В, С, D, F, середины отрезков AD, АВ, если точка А имеет координаты:

вариант 1 (-6; 2,5);

вариант 2 (-3; 6).

Ответ к задачам математического диктанта

Вариант 1. B(-1;2,5); C(-1;-2,5); D(-6; -2,5); F(-3,5; 0); (-6; 0); (-3,5; 2,5).

Вариант 2. В(3; 6); C(3; l); D(-3; l); F(0; 3,5); (-3; 3,5); (0; 6).

II. Восприятие и осознание нового материала

Пусть А(х1; у1), В(х2; у2). Найдем расстояние между точками А и В.

Рассмотрим сначала случай х1 х2, y1 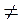y2 (рис. 137).

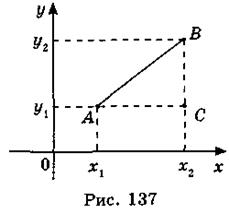
Проведем AC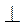BC. В прямоугольном треугольнике ABC имеем:

АС = |х2 - х1|, ВС = |у2 - у1|. По теореме Пифагора имеем: АВ2 = АС2 + ВС2 или АВ = ,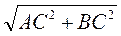

АВ = 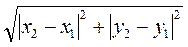= 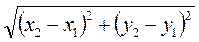. (1)

Если у1 = у2 и х1 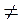х2, то АВ = |х2 - х1|. Такой же результат в этом случае дает и формула (1).

Если х1 = х2 и у1 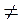у2, то АВ = |y2 - y1|. Такой результат дает и формула (1).

Наконец, х1 = х2, у1 = у2, то есть если точки А и В совпадают, формула (1) дает нужный результат: АВ = 0.

Итак, как бы не были размещены на координатной плоскости точки А(х1; у1), В(х2; у2), всегда имеем: АВ = .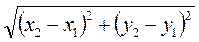

Решение задач

1. 1. Найдите расстояние между двумя точками:

а) А (1) и В (5);

б) А (-5) и В (-1);

в) А (-3) и В (5);

г) А(а) и В(b).

1. 2. Найдите расстояние между двумя точками:

а) А (1; 2) и В (4; 6);

б) А (1; 7) и В (-5; -1);

в) A (a; b) и B (c; d).

III. Закрепление и осмысление нового материала

Решение задач

1. 1. Найдите АВ, если А(-1; 3), В(3; 0). (Ответ. АВ = 5)
2. 2. Найдите расстояние от точки А(-5; 12) до начала координат. (Ответ. ОА = 13)
3. 3. Найдите периметр треугольника ABC, если А(-1; 2), В(3; -1), С(-1; -1). (Ответ. 12)
4. 4. Лежат ли на одной прямой точки А, В, С, если:

а) А(1; 4), В(4; 0), С(2; 2);

б) А(1; 4), В(4; 0), С(2,5; 2)?

(Ответ а) Нет; б) да)

1. 5. Какая из точек А (2; 4) В(-3; 2) - лежит ближе к началу координат? (Ответ. В)
2. 6. Даны точки А (-2; 5), В (1; 8). Найдите точку, равноудаленную от точек А и В, которая лежит:

а) на оси Ох;

б) оси Оу;

в) отрезка АВ.

(Ответ а) (6; 0); б) (0; 6); в) (-0,5; 6,5).)

IV. Домашнее задание

1. 1. Изучить формулу для нахождения расстояния между двумя точками, которые заданы координатами.
2. 2. Решить задачи.
3. 1) Найдите радиус круга, центром которого является точка М(-4; 3), а точка А(-4; 2) лежит на окружности.
4. 2) Найдите периметр треугольника ABC, если А(-1; 3), В(3; 5), С(3; 2).

V. Подведение итогов урока

Вопрос к классу

1. 1. Как найти расстояние между двумя точками на координатной прямой?
2. 2. Как найти расстояние между двумя точками на координатной плоскости?
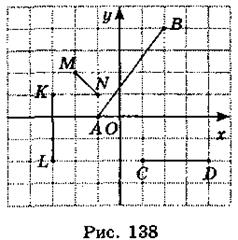
3. 3. Найдите координаты концов каждого отрезка, изображенного на рис. 138, и вычислите его длину.