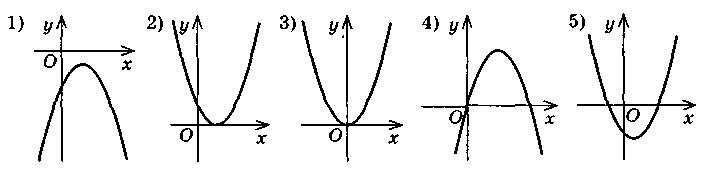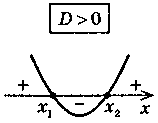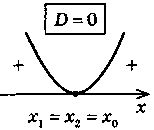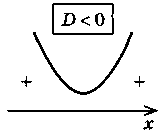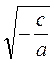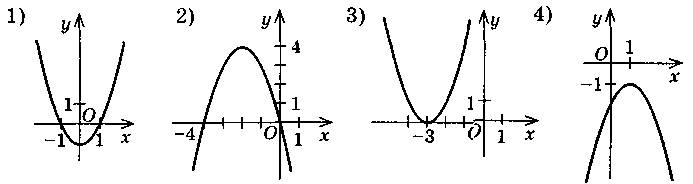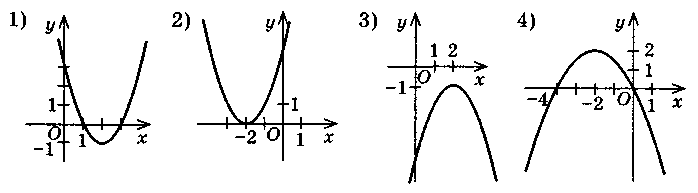УРОК № 24
Тема. Квадратное неравенство. Решение квадратных неравенств
Цель урока: сформировать знания учащихся о содержании понятия «квадратное неравенство», добиться понимания и усвоения учащимися схемы решения квадратных неравенств с использованием построения графика квадратичной функции. Сформировать первичные умения выделять квадратные неравенства среди других неравенств с одной переменной; за готовыми графиками квадратичной функции находить развязки соответствующих квадратных неравенств, а также выполнять последовательные действия в соответствии с изученной схемы для отыскания решений квадратных неравенств различного вида.
Тип урока: формирование знаний, выработка первичных умений.
Наглядность и оборудование: опорный конспект № 17.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Учитель собирает тетради для проверки и оценки качества выполнения домашней самостоятельной работы; ученикам можно раздать правильные решения для самостоятельного анализа ошибок (если такие есть).
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Учитель сообщает ученикам о том, что кроме чисто научного интереса квадратичная функция и построение ее графика имеют свое практическое применение: построение графика квадратичной функции является одним из средств решения неравенств соответствующего вида. Такие неравенства называются квадратных неравенств (или неравенств второй степени). Цель данного урока - изучение определение квадратных неравенств, схемы их решения, а также формирование умений применять изученное определение и схему для того, чтобы отличать квадратные неравенства от других неравенств с одной переменной и находить решения квадратных неравенств.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Среди приведенных уравнений укажите уравнения, задающие квадратичную функцию:
1) у = 2х2 + х - 1;
2) у2 = х + 1;
3) у2 = х2 - 1;
4) у = -х - х2;
5) у2 = х2;
6) у = -х2.
Для указанных функций назовите коэффициенты квадратного трехчлена (в формуле у = ах2 + bх + с).
2. Даны условия:
а) а > 0; D > 0; c 0;
б) а > 0; D = 0; c > 0;
в) а 0; D 0; c 0;
г) а 0; D > 0; c = 0;
д) а > 0; с = 0; D = 0.
Из предложенных рисунков графиков функции у = ах2 + bх + с выберите тот, который удовлетворяет каждую из данных условий:
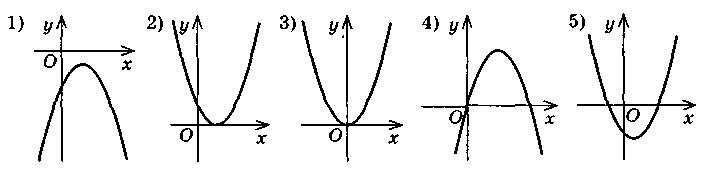
3. Найдите нули функции (если они существуют):
1) у = 2х - 3;
4. 2) у =  ;
;
5. 3) у = 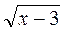 ;
;
6. 4) у = х2 - 3х + 2.
V. Формирование знаний
План изучения нового материала
1. Определение квадратного неравенства. Примеры квадратных неравенств с разными коэффициентами.
2. Схема решения квадратных неравенств с помощью построения графика соответствующей квадратичной функции.
3. Различные способы расположения графика квадратичной функции y = ax2 + bx + c относительно оси Ох в зависимости от знака старшего коэффициента и знака дискриминанта квадратного трехчлена ах2 + bх + с.
Опорный конспект № 17
Неравенства вида ах2 + bх + с > 0 (0; ≥ 0; ≤ 0) называются квадратными, если а 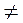 0. 0. |
Пример. 3х2 - 2х - 1 > 0, x2 - 9 ≥ 0, х2 - 2х 0, -х2 > 0 - квадратные неравенства (с различными значениями коэффициентов квадратного трехчлена в левой части). |
Схема решения квадратных неравенств |
1. Найти дискриминантов D, а потом корни x1, x2 квадратного трехчлена (если они существуют). |
2. Построить эскиз графика квадратичной функции у = ах2 + bх + с (с учетом знака коэффициента а и найденного знака дискриминанта D и корней). |
3. Для случая > 0 соответственно получим промежуток, для которого точки параболы лежат выше оси Ох, для случая 0 соответственно получим промежутки, для которых точки параболы лежат ниже оси Ох. |
Схема решения неравенства ах2 + bx + c > 0 в зависимости от а и D |
ax2 + bx + c > 0 (D = b2 - 4ac)
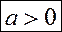
|
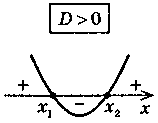
x  (-∞; x1) (-∞; x1)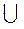 (x2; +∞) (x2; +∞) |
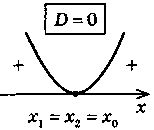
x  (-∞; x0) (-∞; x0)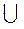 (x0; +∞) (x0; +∞) |
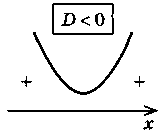
x  R R |
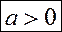
|
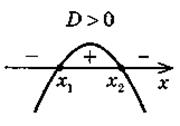
х  (х1; х2) (х1; х2) |
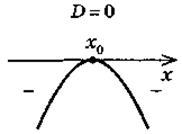
x  (-∞; x0) (-∞; x0) 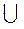 (x0; +∞) (x0; +∞) |
x  R R |
Методический комментарий
Изучение вопроса о решение квадратных неравенств начинается с формирования знаний о содержании определения квадратных неравенств. Следует подчеркнуть, что так же, как и квадратный трехчлен, квадратное неравенство может иметь «сокращенный» вид (см. примеры, приведенные в опорном конспекте № 17). Этот момент является принципиальным, поскольку, как свидетельствует опыт, достаточно большое количество учащихся, решая такие неровности, допускают ошибку: неравенства вида ах2 + с > 0 заменяют на нерівносильну неравенство х > 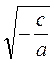 .
.
Схема решения квадратных неравенств осваивается учащимися в 9 классе, поэтому основанная на использовании графика соответствующей квадратичной функции и предусматривает нахождение промежутков постоянства знака функции по эскизу графика.
На этапе формирования умений решать квадратные неравенства по изученной схеме следует требовать от учащихся четкого выполнения следующих действий: свести неравенство к виду квадратной; отыскать действительные корни квадратного трехчлена (если они существуют) и построить эскиз графика квадратичной функции; записать промежуток, на котором функция приобретает знака, что соответствует данной квадратичной неравенства (с учетом строгости знака неравенства).
Предупреждением возможных трудностей учащихся при решении квадратных неравенств является работа с определенного обобщения случаев взаимного расположения графика квадратичной функции относительно координатной оси абсцисс в зависимости от знака старшего коэффициента и знака дискриминанта соответствующего квадратного трехчлена.
VI. Формирование умений
Устные упражнения
1. Даны неравенства:
а) ах2 + bx + c > 0;
б) ах2 + bx + c 0;
в) ах2 + bх + с > 0;
г) ах2 + bx + c 0.
Найдите решение каждой из данных неравенств по графику функции у = ах2 + bх + с, изображенным на рисунке:
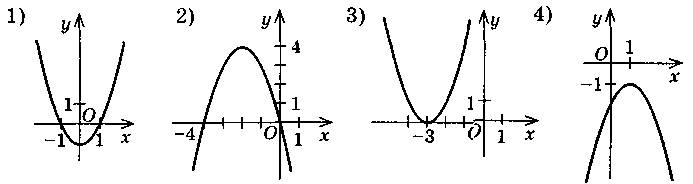
2. Есть число: 0; 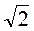 ; -3 - решением неравенства:
; -3 - решением неравенства:
1) 2х + 3 0;
2) х2 ≤ 0;
3) х2 > 2?
3. Какое из неравенств не является квадратной?
1) х2 - 44 > 0;
2) х2 + 3 0;
3) х2 + 3х3 > 0;
4) -х2 - 5 ≤ 0.
Письменные упражнения
Содержание упражнений, предлагаемых к решению на уроке, может быть таким:
1) найти решение квадратного неравенства с готовым графиком соответствующей квадратичной функции;
2) решить по изученной схеме квадратные неравенства;
3) решить неравенства второй степени, сводящиеся к квадратным равносильными преобразованиями;
4) на повторение: установить свойства функции по данному графику этой функции.
Методический комментарий
Упражнения к уроку направленные на усвоение учащимися сформулированного определения квадратного неравенства и выработка умения выделять квадратные неравенства среди других неравенств с одной переменной, опираясь на изученное определения, решения предложенных выше упражнений также будет способствовать усвоению учащимися рассматриваемой схемы решения квадратных неравенств и выработке умений ее применять для отыскания решений как квадратных неравенств, так и неравенств, сводящихся к квадратным путем равносильных преобразований. Решение упражнений на повторение - на применение свойств функции - способствовать подготовке учащихся к предстоящей контрольной работы.
VII. Итоги урока
Контрольные вопросы
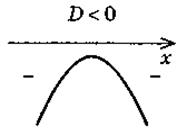
1. Определите знак коэффициента а, коэффициента с, дискриминанта D по графику функции у = ах2 + bх + с, изображенным на рисунке:
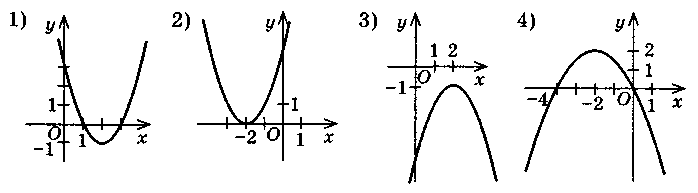
2. Которая квадратное неравенство имеет решением промежуток (см. рисунки выше):
1) x  [1; 3];
[1; 3];
2) x  R;
R;
3) х  (-∞; -4)
(-∞; -4)  (0; +∞);
(0; +∞);
4) решений нет.
VIII. Домашнее задание
1. Изучить определение квадратного неравенства, схему ее решения (см. опорный конспект № 17).
2. Решить упражнения на применение изученного определения и схемы, аналогичные по содержанию и уровню сложности решенным на уроке.
3. Повторить: как найти область определения функции, заданной уравнением вида y = f(x); определение понятие системы неравенств, а также содержание понятия «дискриминантов квадратного уравнения».