АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА
§33. ИСПОЛЬЗОВАНИЕ ГРАФИЧЕСКОГО МЕТОДА РЕШЕНИЯ И ИССЛЕДОВАНИЯ УРАВНЕНИЙ, НЕРАВЕНСТВ И СИСТЕМ.
3. Использование графического метода решения и исследования системы уравнений.
Если задана система уравнений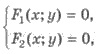 
и
можно построить графики
уравнений F1(x;y) = 0 и F2(х;у)
= 0, то точки пересечения этих графиков и будут решениями системы. Таким образом
можно определить количество решений системы и непосредственно развязки (точно
или приближенно).
Пример. Найдите наибольшее значение
параметра а, при котором система уравнений
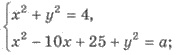имеет единственное решение.
Решения. Запишем систему
следующим образом
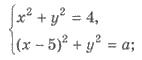
Графиком уравнения х2 + у2
= 4 является круг с центром в точке (0;0) и радиусом 2 (рис.
59). Графиком уравнения (х - 5)2 + у2 = а, где а > 0 является
круг с центром в точке (5;0) и радиусом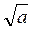 
.
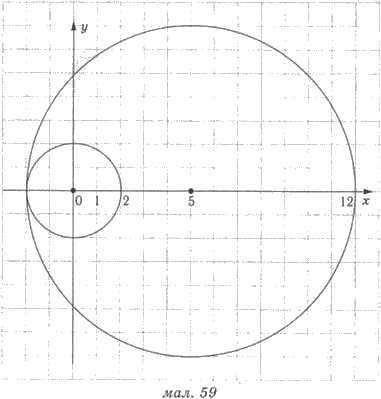
Система будет иметь одно решение, когда
круга дотинатимуться. Наибольшему значению а соответствует внутреннее касание окружностей
(рис. 59). В этом случае
радиус большего круга
равна 7. Следовательно, =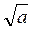
7, а = 49.
Таким образом, наибольшим значением
параметра а при котором система уравнений имеет единственное решение, 49.