АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА
§33. ИСПОЛЬЗОВАНИЕ ГРАФИЧЕСКОГО МЕТОДА РЕШЕНИЯ И ИССЛЕДОВАНИЯ УРАВНЕНИЙ, НЕРАВЕНСТВ И СИСТЕМ.
2. Использование графического метода решения и исследования неровностей.
Если задано неравенство f(x) >
g(х) и построить график
функций у = f(x) и
у = g(x),
то решениями неравенства будут те значения х, для которых график функции у = f(x) расположен
выше, чем график функции у = g(x).
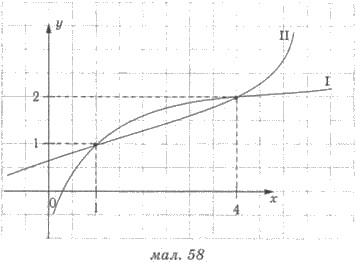
Пример. На рисунке 58 изображен
графики функций f(x) = (2x
+ 12)/14
i g(х) = log4 x +1 Сколько
всего целых решений имеет неравенство f(x) g(x)?
Решения. Сначала по рисунку
надо идентифицировать графики. Поскольку для функции f(x) областью допустимых
значений является множество всех действительных чисел, а для функции g(x) - множество (0;∞), то легко догадаться, что график И -
это график функции g(х) = log4 х +1, а график II - график функции f(x) = (2x
+ 12)/14.
Решениями неравенства f(x) g(x) будут те значения х, для которых график II расположен ниже графика И есть - промежуток
(1;4). На этом промежутке есть два целых числа 2 и 3. Следовательно, неравенство f(х) g(х) имеет два целых решения х = 2 и х = 3.