АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§33. ИСПОЛЬЗОВАНИЕ ГРАФИЧЕСКОГО МЕТОДА РЕШЕНИЯ И ИССЛЕДОВАНИЯ УРАВНЕНИЙ, НЕРАВЕНСТВ И СИСТЕМ.

Мы уже использовали графический метод при решении систем линейных уравнений (§4, п.З) и квадратных неравенств (§14, п.2). Рассмотрим еще пример использования графического метода решения и исследования уравнений, неравенств и систем.

1. Использование графического метода решения и исследования уравнений.

Если задано уравнение f(x) = g(x) и можно построить график функций у = f(x) и у = g(x), то абсциссы пересечения графиков будут решениями уравнения f(x) = g(x). Таким образом можно определить количество решений уравнения f(x) = g(x) и непосредственно развязки (точно или приближенно).

Пример. Сколько решений имеет уравнение х⁶ + х - 3 = 0.

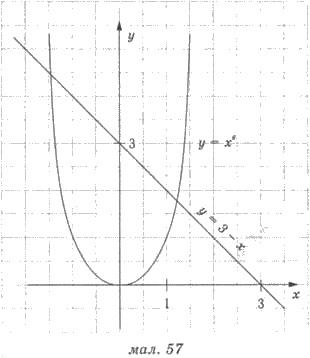
Решения. Представим уравнение в виде х⁶ = 3 - х. Изображаем схематически графики функций у = х⁶ и у = 3 - х (рис. 57). Они пересеклись в двух точках. Поэтому уравнение х⁶+х-3=0 имеет два решения.