АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§32. ПРИМЕНЕНИЕ СВОЙСТВ ФУНКЦИЙ К РЕШЕНИЮ УРАВНЕНИЙ И НЕРАВЕНСТВ.

2. Оценки левой и правой части уравнения или неравенства.

Некоторые виды уравнений вида f(x) = g(x), и неравенств вида f(x) ≤ g(x) удается решить за счет ограниченного левой и правой части уравнений.

Если в уравнении f(x) = g(x) или неравенства f(x) ≤ g(x) для всех значений х из ОДЗ справедливы оценки f(x) ≥ a, g(x) а (где а - некоторое число), то уравнения или неравенства не имеют решений.

Пример 1. Решите уравнение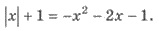

Решения. Поскольку |х| ≥ 0 для всех значений х, то |х| + 1 ≥ 1. С другой стороны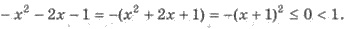

Следовательно, 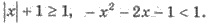Поэтому уравнение не имеет решений.

Если в уравнении f(x) = g(x) или неравенства f(x) ≤ g(x) для всех значений х из ОДЗ справедливы оценки f(x) ≥ а, g(x) ≤ а, то уравнение или неравенство равносильно системе

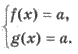
Пример 2. Решите неравенство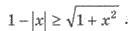

Решения. ОДЗ этого неравенства состоит из всех действительных чисел. Оценим левую часть неравенства |х| ≥ 0; -|х| ≤ 0; 1-|х| ≤ 1. Оценим правую часть неравенства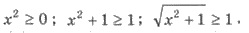

Итак, 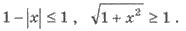Поэтому начальная неравенство равносильна системе:

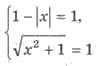откуда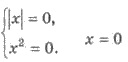

Следовательно, х = 0 - единственное решение неровности.