АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§32. ПРИМЕНЕНИЕ СВОЙСТВ ФУНКЦИЙ К РЕШЕНИЮ УРАВНЕНИЙ И НЕРАВЕНСТВ.

1. Использование ОДЗ уравнения или неравенства, которое является пустым множеством или конечным множеством.

Легко понять, что каждый развязок уравнения или неравенства должен принадлежать ОДЗ всего уравнения или неравенства. Поэтому, если ОДЗ уравнения или неравенства является пустым множеством, то уравнение или неравенство не имеет корней.

Пример 1. Решите неравенство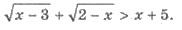

Решения. ОДЗ неравенства задается системой 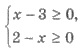откуда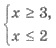

Последняя система не имеет решений, ОДЗ неравенства является пустым множеством (не содержит ни одного числа), поэтому неравенство решений не имеет.

Иногда ОДЗ уравнения или неравенства является конечной множеством, то есть в ОДЗ входят несколько чисел (в основном одно-два числа).

Если ОДЗ уравнения или неравенства является конечной множеством, то для его решения достаточно проверить все числа, входят в ОДЗ.

Пример 2. Решите уравнение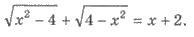

Решения. ОДЗ уравнения задается системой

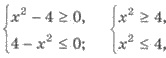
т.е. х² =4, x₁ = 2; х₂ = -2.

Проверим по очереди эти значения:

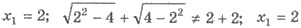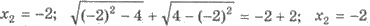- не является корнем уравнения;

- корень уравнения.

Следовательно, х = -2 - единственный корень уравнения.