Урок № 22
Тема. Свойства степени (продолжение). Доля степеней с одинаковым основанием
Цель: добиться сознательного понимания учащимися свойств степени с натуральным показателем (доля степеней) и выработать умения применять эти свойства для упрощения выражений вместе с другими свойствами степени, изученными ранее.
Тип урока: усвоение знаний, умений и навыков.
Ход урока
I. Проверка домашнего задания. Актуализация опорных знаний
Блиц-контроль
1. Какое из равенств является правильной:
1) 24 · 23 = 212;
2) 24 · 23 = 412;
3) 24 · 23 = 47;
4) 24 · 23 = 27?
2. Запишите в виде степени с основанием х:
1) х5 · x3;
2) х4 · x;
3) х4 · х5 · х;
4) хn · х · хm.
3. Запишите в виде степени с основанием 2: 22n · 4:
1) 82n; 2) 22n+1; 3) 62n; 4) 22n+2.
После проведенного блиц-контроля проверяем качество его выполнения и предлагаем ученикам объяснить выполненные действия (повторяем основное свойство степени; определение степени с натуральным показателем).
II. Работа с опережающим домашним заданием
Задачи:
1) Известно, что ab = с. Какие правильные равенства вытекают из данного равенства? При каких а и b это будет правильным?
2) Известно, что а3 · a2 = а5. Какие правильные равенства вытекают из нее? При каких условиях эти равенства будут правильными?
@ Понятно, что большинство учащихся с заданием 1) справится легко, потому что если ab = с, то 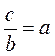 ,
, 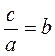 (а и b не равны 0).
(а и b не равны 0).
Если эта часть задачи выполнена, то задача 2) по аналогии приводит к выводам:
Если а3 · а2 = а5, то а5 : а2 = а3 (*); а5 : а3 = а2 (**), если ни а3, ни а2 не равны нулю.
III. Усвоение знаний
@ Добиться сознательного понимания учащимися следующей свойства можно, выполнив работу из сравнения по алгоритму (см. приложение) полученных выражений: а3 · a2 = a5; a5 : a2 = а3; а5 : а3 = а2.
После проведенного сравнения и коррекции выполненной учащимися самостоятельной работы приходим к выводам:
1) Во время деления степеней с одним основанием основа не меняется, а от показателя делимого вычесть показатель делителя. (Если показатель делимого больше показатель делителя.)
2) Основание степени при делении должна быть отличной от 0.
Особые случаи применения этого свойства выводим из практических задач.
Задачи. Упростите выражение. 1) а5: а5; 2) а5 : а7.
Снова обращаемся к сравнения, а из этого возникает необходимость уточнения сформулированной свойства, а именно:
1) если аm · аn = а0 = 1, т.е. а0 = 1 (а ≠ 0);
2) если m n, то 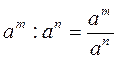 и делим
и делим 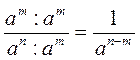 .
.
Все выводы учеников записывают в тетради в сжатом виде.
Конспект 8 |
Деление степеней с одинаковым основанием |
Если 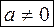 и: и: |
1) m > n, то 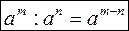 2) m = n, то 2) m = n, то 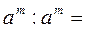 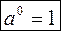 |
3) m n, то 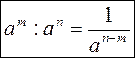 |
Примеры: а6 : а2 = а6 - 2 = а4; 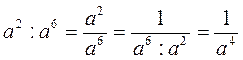 ; а2 : а2 = а2 - 2 = а0 = 1 ; а2 : а2 = а2 - 2 = а0 = 1 |
IV. Применение знаний
@ На этом уроке концентрируем внимание на понимании учащимися свойства степени, что следует из основного свойства степени. Поэтому не требуем от учеников воспроизведения алгоритмов, но объяснять действия учащиеся должны.
Выполнение устных упражнений
1. Объясните, почему действия выполнены именно так:
1) а8 : а4 = а8 - 4 = а4;
2) 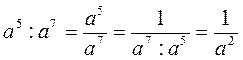 ;
;
3) а8 : а8 = а8 - 8 = а0 = 1.
Каким является значение а (по смыслу задачи)?
2. Какое из равенств является неправильной:
1) 27 : 25 = 22 = 4;
2) 37 : 36 = 1;
3) 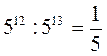 ; 4) 52 : 25 = 1?
; 4) 52 : 25 = 1?
3. Представьте в виде степени долю:
1) a8 : a2; 2) 34 : 3; 3) x6 : x; 4) 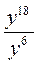 ; 5) -z6 : (-z)3.
; 5) -z6 : (-z)3.
4. Какое выражение надо поставить вместо *, чтобы получить правильное равенство: a15 : * = a5?
Выполнение письменных упражнений
1. Представьте в виде степени долю:
1) a21 : a17;
2) b9 : b;
3) b11 : b11;
4) (a - b)15 : (a - b)11.
2. Замените * степени с основанием а, чтобы равенство было верным:
1) а14 : * = а6;
2) * : а11 = а21;
3) * : а7 · а11 = а18;
4) а9 : * : а = а3.
3. Вычислите значения выражений (в случае необходимости обращаемся в справочных таблиц).
1) 22 · 23;
2) 315 : 311;
3) 59 · 53 : 516;
4) 1111 : 1110 · 11;
5) 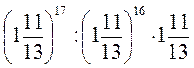 ;
;
6) 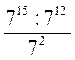 ;
;
7) 32 : 81; 8) 256 : 25 · 22.
4. Представьте в виде степени выражение (n - натуральное число):
1) х27 : х, n ≤ 17;
2) хn : (х10 : х12), n ≥ 7;
3) x5n : x3n · х4n+2;
4) (х3 ·х3n)(х2n · х2n).
V. Итог урока. Рефлексия
Закончите предложения, чтобы они стали истинными:
1) Чтобы поделить 25 на 23, надо...
2) Чтобы поделить 37 на 310, надо...
3) Чтобы поделить на 715 715, надо...
VI. Домашнее задание
№ 1. Представьте в виде степени:
1) a12 : a4;
2) c8 : c;
3) b5 : b5;
4) (a+b)n : (a+b)7;
5) 313 :36;
6) 75 · 712 : 714;
7) 378 : 377 · 37;
8) 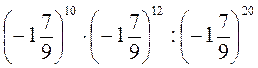 ;
;
9) х3n : х2п · х5n-1.
№ 2. Вычислите значение выражения:
1) 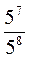 ; 2)
; 2) 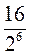 ; 3)
; 3) 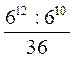 ; 4)
; 4) 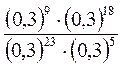
№ 3. Опережающее домашнее задание. Что называют степенью числа с натуральным показателем? Что называют основанием степени? показателем степени? (Найдите в учебнике.)
Используя знания, приобретенные ранее, назовите основание и показатель степени, прочитайте выражение с помощью слов и запишите выражение в виде произведения:
а5
(а2)5
(аn)5
(аn)m
Какое свойство умножения можно использовать, чтобы упростить образован произведение? Выполните умножение и сравните ответы. К какому выводу вы пришли?
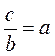 ,
, 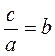 (а и
(а и 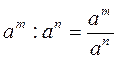 и делим
и делим 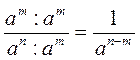
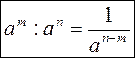
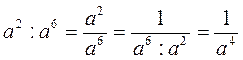
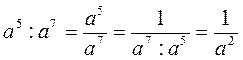
 ;
; 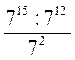 ;
;