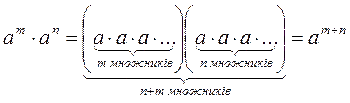Урок № 21

Тема. Свойства степени с натуральным показателем. Произведение степеней с одинаковым основанием

Цель: добиться сознательного понимания учащимися свойства умножения степеней с одним основанием и сформировать умение преобразовывать числовые и буквенные выражения с использованием этого свойства.

Тип урока: усвоение знаний, умений и навыков.

Ход урока

I. Проверка домашнего задания

(Собрать тетради)

II. Актуализация опорных знаний

Выполнение устных упражнений

1. Какие из выражений с степенью с натуральным показателем?

23; 2-5; 2 · (-5); (-5)2; -5 · (-2); (-5)-2.

Для степеней с натуральным показателем назовите основание и показатель. Как записать эти степени в виде произведения? Вычислите значение степени.

2. Не вычисляя значения выражений, сравните их с нулем:

(-5)13; (-5)12; -512; (х - 1)12; (х - 1)13 ; -(х - 1)12.

Какие соображения вы использовали?

3. Найдите квадраты, кубы, 4 и 5-е степени чисел 2 и 3, заполните таблицу:

III. Работа с опережающим домашним заданием

Задачи. Докажите, что произведение а3 и а2 равен а5.

@ Учащиеся используют алгоритм доказывания (см. приложение и рассуждения, которые были использованы во время выполнения опережающего домашнего задания).

Приложение

Алгоритм доведения

1. Учреждения и сформулируй проблему, которую надо доказать.

2. Дай определение понятиям, с помощью которых будет осуществляться доведение.

3. Подбери достаточно основательные аргументы.

4. Определи способ и логику доказательства.

5. Сделай вывод.

Аргументы (основания) - суждения, истинность которых проверена и доказана практикой. Главной характеристикой является истинность, то есть соответствие действительности.

@ Понятно, что выполнение этой работы будет легким для учеников, потому что в опережающем задании есть намек на те действия, предусмотренные алгоритмом. Поэтому по выполнении этого задания не возникает сомнения в том, что a3 · a2 = a5.

Сравните левую и правую часть равенства. Сформулируйте гипотезу.

IV. Усвоение знаний. Проблемная ситуация

Задача 1. Доказать, что а5 · а8 = а13; а · а12 = а13.

Задание 2. Доказать, что а13 · а27 = а40.

Задача 3. Как представить в виде степени произведение а135 · а247 ?

1) Осознаем суть всех заданий: по аналогии с решенными ранее пытаемся доказать, что произведение двух степеней с одним основанием является степенью с той же основой, а показатель - сумма показателей множителей.

2) Выбираем способ доведения (по аналогии с опережающим домашним заданием), но, чтобы «обобщить» запись, заменяем числовые показатели буквами и формулируем утверждение, что является основой для решения задач 1-3.

Докажите, что аn · аm = аn+m, если а - любое число; m и n - натуральные числа.

Докажите (по аналогии с алгоритмом и доведенного равенством а3 · а2 = а5) может провести учитель или предложить выполнить учащимся.

Запись в тетрадях может иметь такой вид:

V. Применение знаний, умений и навыков

@ Задание на закрепление понимания учащимися основного свойства степени (аm · аn = аm+n) предусматривают:

1) закрепление терминологии;

2) усвоение умений преобразовывать произведение степеней с одинаковым основанием в степень;

3) усвоение умений преобразовывать степень на произведение степеней с одним основанием;

4) повторение изученных свойств степеней с четными и нечетными показателями.

Поэтому система заданий, что поможет учителю и учащимся достичь определенной цели, может быть такой:

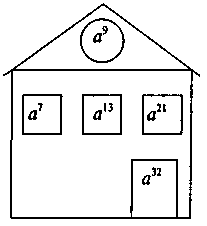
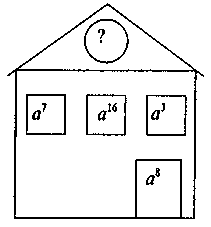
Выполнение устных упражнений

1. Из произведений выражений можно представить в виде степени с использованием основного свойства степени:

а3 · а5; а3 · b5; а3 · а2 · а7; (а + b)2(а + b)3; 3m ·3n; 32 · 92; m3 · n3?

Почему?

2. Представьте выражение в виде степени:

х5 · х7; 5 · 52; а · а3; у4 · у6 · в; 102 ·10 · 103; с · с · с3; z · z5; 74 · 49; (-6) · (-6)3 · (-6); a2n · an.

3. Какое выражение надо поставить вместо *, чтобы равенство а2 · а* = а6 была правильной? Почему?

Выполнение письменных упражнений

1. Представьте в виде степени произведение:

1) m5 · m3;

2) х · х6;

3) а4 · а4;

4) 54 · 54;

5) у3 · в8 · у5;

6) с7 · с · с2;

7) (m - n)8(m - n)3;

8) (u + v)3·(u + v);

9) (a - b)(a - b)(a - b)2;

10) х2п · х2n-2;

11) хn · х5.

2. Замените * на степень так, чтобы равенство стало верным:

1) a8 · * = a13;

2) a11 · * · a = a16.

3. Найдите значение переменной, при котором будет верным равенство:

1) 45 · 43 = 45+х;

2) 23 · 22 = 21+x;

3) 2n · 25 = 27;

4) 34 · 3n = 37;

5) 75 · 7x = 72х-1;

6) 75 · 7x = 715-2х.

4*. Упростите выражение:

1) а10 · а12 ·(-а5);

2) х · (-х) · (-х6);

3) вn · в8 · у2;

4) bn · bn · b3.

5*. Представьте в виде произведения двух множителей, один из которых а5, такие выражения:

1) a10; 2) a6; 3) -a40.

6*. Представьте в виде степени выражение: 1) 25 · 8; 2) 4 · 8; 3) 7n · 49; 4) 27 · 3n.

@ Перед выполнением сравним условия упражнения № 6 с развязанными предварительно и найдем различие (множители если и есть степенями, то с разными основами), следовательно, опираясь на № 3 представленных упражнений, заменяем множитель(ы) степенями с одинаковыми основами и используем основное свойство степени.

7. Логическое упражнение. Найдите пропущенные записи:

V. Итоги урока. Рефлексия

На отдельных карточках записаны этапы использования основного свойства степени для упрощения выражений; карты предлагаются ученикам в хаотичном порядке, например:

Ученикам предлагается установить правильный порядок действий при поиске ответов на вопросы:

Как найти произведение степеней с одним основанием?

VI. Домашнее задание

№ 1. Представьте в виде степени произведение:

1) а9 · а2; 2) а · а7; 3) b3 · b3; 4) 711 · 73; 5) m4 · m5 · mn; 6) c19 · с · сn; 7) (a+b)(a+b)7; 8) n9 · n4 ·nk+1 ·n.

№ 2. Замените * степени с основанием а, чтобы образовалась правильная равенство:

1) а11 · * = a13; 2) a3 · * · a = a25.

№ 3. Представьте в виде степени: 1) 58 · 25; 2) 312 · 27; 3) 29 · 16.

№ 4. Опережающее домашнее задание. Какие правильные равенства можно записать из того, что a · b = c?

(Как найти множитель а; множитель b?)

Какие равенства, соответственно, вытекают из того, что а3 · а2 = а5

(при условии, что а≠0)?

Как прочитать эти равенства словам?