Урок 23

Тема. Решение задач

Цель урока: обобщение и систематизация знаний, умений и навыков учащихся по теме «Параллельность прямых и плоскостей».

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания

1. Два ученика воспроизводят решения задач № 39, 40, а в это время класс пишет математический диктант.

2. Математический диктант.

Задан параллельную проекцию A1B1C1

(вариант 1 - рис. 107; вариант 2 - рис. 108) равнобедренного треугольника АВС (АВ = АС ≠ ВС).

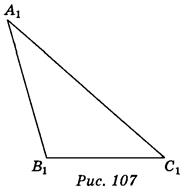
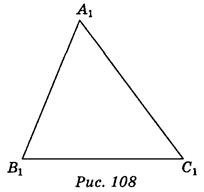
1) Постройте проекцию D1 точки D, которая является серединой отрезка АС. (2 балла)

2) Постройте проекцию C1F1 медианы CF треугольника АВС. (2 балла)

3) Постройте проекцию А1К1 биссектрисы АК треугольника АВС. (2 балла)

4) Постройте проекцию средней линии треугольника, параллельной стороне ВС. (2 балла)

5) можно Ли отрезок B1D1 считать проекцией высоты треугольника АВС? (2 балла)

6) можно Ли отрезок D1K1 считать проекцией средней линии DK? (2 балла)

Ответ. Вариант 1. 1-4) - рис. 109; 5) нет; 6) да.

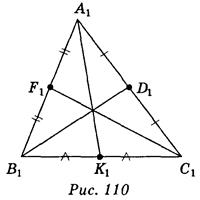
Вариант 2. 1-4) - рис. 110; 5) нет; б) да.

3. Проверка выполнения математического диктанта, заслушивание учащихся, которые воспроизводили решения задач № 39, 40 и ответы на вопросы, которые возникли у учащихся при выполнении этих задач и написании математического диктанта.

II. Закрепление и осмысление знаний учащихся

Решение задач

1. Параллелограмм ABCD не имеет общих точек с плоскостью α. Через точки А, В, С, D проведены параллельные прямые, пересекающие плоскость соответственно в точках А1, В1, С1, D1.

а) Что можно сказать о плоскости АВВ1A1 и CDD1C1?

б) Определите вид четырехугольника A1B1C1D1.

2. Даны параллельные плоскости α и β. Через точку S, не принадлежащая ни одной из них, проведены прямые а и b, которые пересекают плоскость α в точках A1 и B1, а плоскость β - в точках А2 и B2, причем SA1 = 8 cm, А1А2 = 12 cm, A2B2 = 25 cm. Найдите А1B1. (Ответ. 10 или 50 cm)

3. Прямые а и b пересекают три данные параллельные плоскости в точках А1, А2, А3 и В1, В2, B3 соответственно (точка A2 лежит между точками А1 и А3, а точка B2 - между точками В1 и B3). Известно, что А1А2 = 12 см, В2В3 = 27 см и А2А3 = В1В2. Найдите длину отрезков А1А3 и В1В3. (Ответ А1А3 = 30 см, В1В3 = 45 см)

4. Три параллельные плоскости пересекают две скрещивающиеся прямые в точках A1, А2, А3 и В1, B2, B3 соответственно (точка А2 лежит между точками A1 и А3, точка В2 - между точками В1 и B3). Известно, что А2А3 = 8 см, В1В2 = 18 см и А1A2 + В2В3 = 24 см. Найдите длины отрезков А1А3 и B1B3. (Ответ. А1А3 = 20 см, В1В3 = 30 см)

5. Задача № 21* из учебника (с. 20).

6. Задача № 34* из учебника (с. 21).

III. Домашнее задание

Задачи № 26, 41 (с. 20, 22). Подготовиться к тематической аттестации № 2.

IV. Подведение итога урока

Вопрос к классу

1. Прямые а и b, которые пересекаются, пересекают три даны параллельные плоскости α, β, γ в точках А1, А2, А3 и В1 В2, В3 соответственно (рис. 111). Определите, какие из приведенных утверждений правильные, а какие - неправильные:

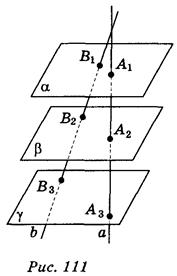
а) прямые А2В2 и А3В3 скрещивающиеся;

б) прямые А1В3 и А3В1 скрещивающиеся;

в) прямая b и точки А1, А2 обязательно лежат в одной плоскости;

г) А1А3 : A1A2 = В1В2 : В1В3;

д) А1А2 : В1В2 = A1A3 : В1В3.

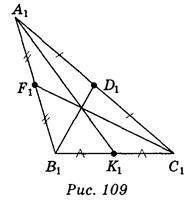
2. Три параллельные плоскости α, β, γ пересекающих две данные скрещивающиеся прямые а и b в точках А1, А2, А3 и В1, B2, В3 соответственно (рис. 112). Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) прямые А1B3 и В1А3 пересекаются;

б) если А2А3 = 1 см, В1В2 = 4 см, A1A2 = В2В3, то В1В3 = 5 см;

в) прямые А2В2 и А3В3 могут быть параллельными;

г) А1А3 : В1В3 = А2А3 : В2В3.