Урок 22

Тема. Решение задач

Цель урока: формирование умений строить изображения пространственных фигур, используя свойства параллельного проектирования.

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания

Фронтальное опрашивание.

1) Что можно сказать про параллельную проекцию прямой на плоскость?

2) Что можно сказать о проекции параллельных прямых на плоскость?

3) Точка С делит отрезок АВ в отношении АС : СВ = 2 : 3. Параллельными проекциями точек А, В, С на плоскость а будут точки А1, B1, С1. В каком отношении точка С1 делит отрезок А1В1 ?

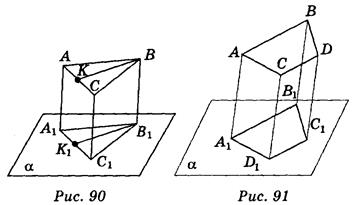
4) Треугольник А1В1С1 - параллельная проекция треугольника АВС на плоскость α (рис. 90). Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) если треугольник АВС правильный, то треугольник А1В1С1 обязательно правильный;

б) треугольник АВС не может быть равен треугольнику А1В1С1;

в) если ВК - биссектриса треугольника АВС, то B1K1 обязательно - биссектриса треугольника А1В1С1;

г) если ВК - медиана треугольника АВС, то В1К1 обязательно - медиана треугольника A1B1C1.

5) Объясните решение задачи № 38.

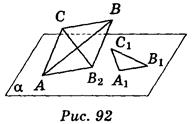
6) Четырехугольник A1B1C1D1 является параллельной проекцией рівнобічної трапеции ABCD (АВ - основание трапеции) на плоскость α (рис. 91). Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) прямые A1D1 и В1С1 могут быть параллельными;

б) прямые A1B1 и D1C1 могут пересекаться;

в) отрезки А1D1 и В1С1 могут быть равными;

г) отрезки А1В1 и D1C1 могут быть равными;

д) если 2АВ = 3DC, то 3А1В1 = 2D1C1.

II. Закрепление и осмысление знаний учащихся

Формирование умений строить изображения фигур

Остановимся на изображении наиболее применяемых геометрических фигур, из комбинаций которых состоит, как правило, изображения любой сложной пространственной фигуры.

ИЗОБРАЖЕНИЕ ТРЕУГОЛЬНИКА

Любой треугольник может быть изображением треугольника произвольной формы, в частности: правильного, равнобедренного, прямоугольного.

Доведение

Пусть задан треугольник АВС произвольной формы и на плоскости проекции α задан треугольник А1В1С1. Всегда можно расположить треугольник АВС и выбрать направление проектирования так, что треугольник проецируется в треугольник, подобный треугольнику А1В1С1 (рис. 92). Построим треугольник AB2C, который подобен треугольнику А1В1С1 выбрав за направление проектирования прямую BB2, получим, что ΔАВС проектируется в ΔАВ2С такой, что ΔАВС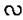ΔА1В1С1.

Следует отметить, что медианы и средние линии треугольника изображают соответственно медіанами и средними линиями изображения.

Задача.

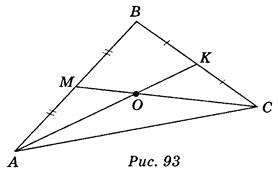
На изображении равностороннего треугольника постройте изображение его центра.

Решение

Пусть АВС (рис. 93) - данное изображение равностороннего треугольника. Центр правильного треугольника - точка пересечения его медиан. Поэтому, построив медианы АК и CM на изображении, которые пересекутся в точке О, получим: точка О - центр правильного треугольника АВС.

ИЗОБРАЖЕНИЕ ПАРАЛЛЕЛОГРАММА

Изображением параллелограмма (прямоугольника, ромба, квадрата) можно считать произвольный параллелограмм, принадлежащей плоскости проекций.

Действительно, пусть ABCD - параллелограмм, что проектируют, тогда произвольный треугольник А1В1С1 можно считать проекцией треугольника АВС (рис. 94). Учитывая, что при параллельном проектировании параллельные отрезки переходят в параллельные отрезки, и проведя A1D1 || В1С1 и C1D1 || А1В1, получим A1B1C1D1 - параллелограмм, который является изображением параллелограмма ABCD (в частности, прямоугольника, ромба, квадрата).

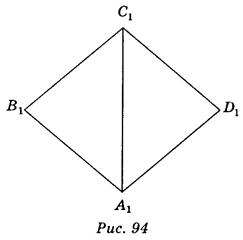
Задача.

Постройте изображение ромба с углом 120° и изображение высоты ромба, проведенная из вершины этого угла.

Решение

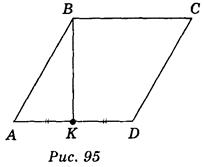
Пусть параллелограмм ABCD (рис. 95) является изображением ромба A1B1C1D1, у которого B1 = 120° (рис. 96).

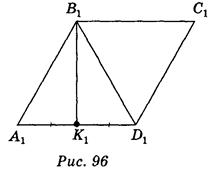
Поскольку ΔА1В1D1 - равносторонний, то его медиана В1K1 является одновременно и высотой этого треугольника, а следовательно, и ромба.

Таким образом, построив середину стороны AD и соединив эту точку с вершиной В, получим ВК - изображение высоты (см. рис. 95).

ИЗОБРАЖЕНИЕ ТРАПЕЦИИ

Из свойства параллельного проектирования следует, что изображением трапеции есть трапеция, у которой отношение длин оснований изображения равно отношению длин оснований трапеции, которую проектируют.

Задача.

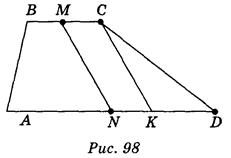
Постройте изображение рівнобічної трапеции с основаниями 3 и 9 см и изображения ее высоты.

Решение

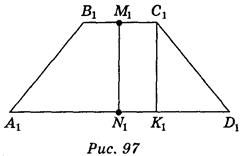
Пусть A1B1C1D1 - равносторонняя трапеция, у которой А1D1 || В1С1, A1D1 = 9 см, В1С1 = 3 см. Следует отметить, что высота С1К1 параллельна оси симметрии М1N1 (точки М1 и N1 - середины оснований трапеции) (рис. 97). Но при параллельном проецировании сохраняются параллельность прямых и отношение длин параллельных отрезков. Отсюда вытекает построение: трапеция ABCD, в которой AD || ВС и AD = 3 ВС, является изображением трапеции (рис. 98); построив точки М и N - середины сторон ВС и AD и СК || MN, получим отрезок СК - изображение высоты трапеции.

ИЗОБРАЖЕНИЕ ЧЕТЫРЕХУГОЛЬНИКА

Изображением произвольного четырехугольника (параллелограмма и трапеции) есть произвольный четырехугольник.

ИЗОБРАЖЕНИЕ ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА

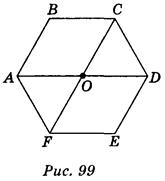
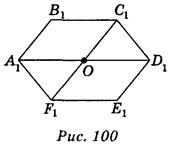
Рассмотрим правильный шестиугольник ABCDEF (рис. 99). Точка О пересечения диагоналей AD и FC - его центр симметрии, поэтому ромба АВСО и DEFO симметричны относительно точки О. Ромб АВСО изображаем в виде произвольного параллелограмма A1B1C1D1 (рис. 100). Для построения последних вершин изображение достаточно построить точки D1, E1, F1, соответственно симметричны относительно точки О1 точкам А1, B1, С1.

ИЗОБРАЖЕНИЕ КРУГА

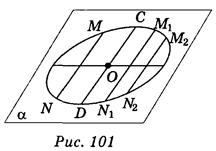
Изображением круга с центром в точке О1 является эллипс с центром в точке О, который принадлежит плоскости проекции α. Каждый диаметр эллипса АВ делит пополам хорды MN, M1N1, M2N2 ..., параллельные сопряженного с ним диаметра CD (рис. 101).

Следует отметить, что сопряженными диаметрами эллипса называются изображения двух перпендикулярных диаметров круга, что проецируется.

Решение задачи № 42 из учебника (с. 22).

ИЗОБРАЖЕНИЕ ТЕТРАЭДРА

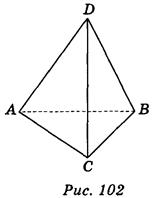
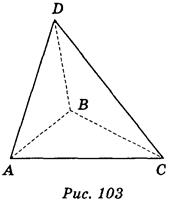
Рассматривая тень, что дают на экране каркасная модель тетраэдра, можно сформулировать правило его изображение. Изображением ребер данного тетраэдра могут быть стороны и диагонали произвольного выпуклого (рис. 102) или невыпуклого четырехугольника ABCD (рис. 103).

ИЗОБРАЖЕНИЕ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА

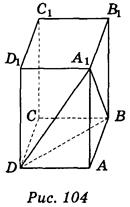
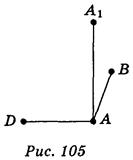
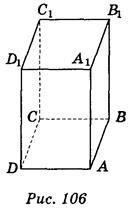
Пусть задан прямоугольный параллелепипед ABCDA1B1C1D1. Выберем три его ребра АВ, AD и АА1, имеющих общее начало (рис. 104). Рассмотрим тетраэдр A1ABD. Пользуясь правилом изображения тетраэдра, приходим к выводу, что ребра АВ, AD, AA1 можно изобразить в виде трех произвольных отрезков, выходящих из одной точки (рис. 105). Последние его ребра следует изобразить определенными отрезками, каждый из них параллельный одном из построенных отрезков и равен ему по длине (рис. 106).

III. Домашнее задание

§2, п. 13; контрольный вопрос № 12; задачи № 39, 40 (с. 22).

IV. Подведение итога урока

Вопрос к классу

1. Четырехугольник A1B1C1D1 является параллельной проекцией трапеции ABCD (AD - основание трапеции) на некоторую плоскость. Укажите, какие из указанных утверждений правильные, а какие - неправильные:

а) четырехугольник A1B1C1D1 является трапецией с основанием C1D1;

б) четырехугольник А1В1C1D1 может быть ромбом;

в) четырехугольник A1B1C1D1 является трапецией с основанием А1D1;

г) четырехугольник A1B1C1D1 является трапецией с основанием В1D1;

д) если ВС = 5AD, то 5В1C1 = A1D1.

2. Четырехугольник A1B1C1D1 является параллельной проекцией прямоугольника ABCD на некоторую плоскость. Укажите, какие из перечисленных утверждений являются правильными, а какие - неправильными:

а) в четырехугольнике A1B1C1D1 является параллельные стороны;

б) в четырехугольнике А1B1С1D1 обязательно есть равные стороны;

в) четырехугольник A1B1С1D1 может быть трапецией;

г) диагонали четырехугольника A1B1C1D1 точкой пересечения делятся пополам;

д) диагонали четырехугольника А1B1С1D1 уровне обязательно.