АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА
§29. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА.
2. Неравенства вида loga f(x) ≥ loga g(x), loga f(x) > loga g(x).
Представим метод решения
неравенства loga f(x) ≥ loga g(x) в виде таблицы:
|
loga f(x) ≥ loga g(x)
|
|
0 а 1
|
а > 1
|
|
Знак неравенства меняется на
противоположный
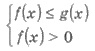
|
Знак неравенства не меняется
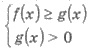
|
Неравенство вида loga f(x) > loga g(x) решается
аналогично.
Пример. Решите неравенство:
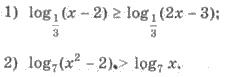
Решения. 1) Поскольку 0 1/3 1, то знак неравенства меняем
на противоположный х - 2 ≤ 2х
- 3. Кроме того надо учесть х -
2 >
0 (тогда условие 2х - 3
> 0 будет выполняться автоматически). Следовательно, неравенство равносильно системе:
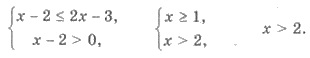
2) Поскольку 7 > 1, то знак
неравенства не меняем х2 - 2 > х. Кроме того надо учесть х > 0 (условие х2
- 2 > 0 выполняется автоматически).
Итак, имеем:
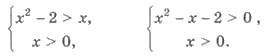
Решения первого неравенства: х
-1 и х > 2 (рис. 49 - схема вверху). Учитывая х > 0, имеем решения: х
> 2.
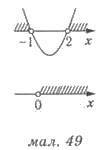
Следовательно, решением начальной
неравенства является множество: х > 2.