Урок № 22
Тема. Равнобедренный треугольник
Цель: осуществить
диагностику усвоения знаний и умений по теме «Первый и второй признаки равенства
треугольников».
Добиться сознательного
понимание учащимися:
·
определение
равнобедренного треугольника, названия его элементов;
·
определение
равностороннего треугольника и того факта, что равносторонний треугольник можно
считать равнобедренным; теорему, выражающую свойство углов при основании
равнобедренного треугольника.
Сформировать первичные
умения:
·
используя
определения, распознавать на рисунке или по условию равнобедренный треугольник и
называть его элементы;
·
воспроизводить
теорему о свойстве углов при основании равнобедренного треугольника и
использовать условие теоремы при решении задач.
Наглядность и
оборудование: набор
демонстрационного чертежных принадлежностей; таблица «Равнобедренный треугольник».
Таблица
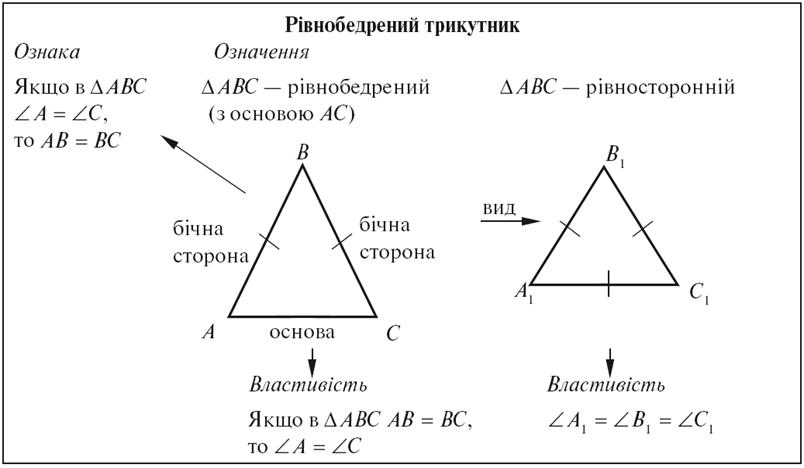
ХОД УРОКА
I. Организационный
момент
II. Проверка
домашнего задания
Тетради с домашним
задачей учитель собирает вместе с выполненной в них самостоятельной работой.
Самостоятельная
работа
Вариант 1
Начальный уровень
1. В треугольниках ABC и
KNM AB = KN, AC = KM, 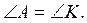 Докажите, что ΔABC =ΔKNM.
Докажите, что ΔABC =ΔKNM.
Средний уровень
2. В треугольниках ABC и
BAD 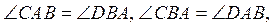 AD =
2 см. Найдите BC.
AD =
2 см. Найдите BC.
Достаточный уровень
3. Отрезки AM и BN -
расстояния от точек A и B до прямой MN. Известно, что AM = BN. Докажите, что 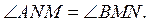
Высокий уровень
4. Отрезок AB является
перпендикулярным до отрезка CD и проходит через его середину. Докажите
равенство треугольников ABC и ABD.
Вариант 2
Начальный ровень
1. В треугольниках ABC и
XYZ 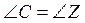 , BC =YZ,
AC = XZ. Докажите, что ΔABC =ΔXYZ.
, BC =YZ,
AC = XZ. Докажите, что ΔABC =ΔXYZ.
Средний геь
2. В треугольниках ABC и
ABD 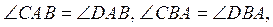 BC
= 8 см. Найдите BD.
BC
= 8 см. Найдите BD.
Достаточный геь
3. Отрезки AM и BN -
расстояния от точек A и B до прямой MN. Известно, что 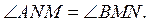 Докажите, что AM = BN.
Докажите, что AM = BN.
Высокий ривэнь
4. Отрезок CD является
перпендикулярным к отрезка AB и проходит через его середину. Докажите
равенство треугольников ACD и BCD.
Вариант 3
Начальный ровень
1. Две прямые
пересекаются в точке O. На одной прямой от точки O отложены равные отрезки OA
и OB, а на второй прямой - равные отрезки OC и OD. Докажите равенство
треугольников OAC и OBD.
Средний геь
2. Отрезок CD проходит
через середину O отрезка AB так, что 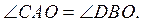 Найдите AC, если BD = 8 см.
Найдите AC, если BD = 8 см.
Достаточный геь
3. В треугольнике 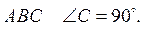 Расстояние от
точки A до прямой BC равно 3 см, а от точки B до прямой AC - 4 см. Найдите периметр треугольника ABC, если AB = 5 см.
Расстояние от
точки A до прямой BC равно 3 см, а от точки B до прямой AC - 4 см. Найдите периметр треугольника ABC, если AB = 5 см.
Высокий ривэнь
4. В треугольнике 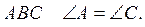 На сторонах AB и CB
отложены равные отрезки AM и CN. Докажите, что ΔANB =ΔCMB.
На сторонах AB и CB
отложены равные отрезки AM и CN. Докажите, что ΔANB =ΔCMB.
Вариант 4
Начальный ровень
1. На сторонах угла O отложено
равные отрезки OA и OB. Луч OC - биссектриса угла O. Докажите равенство
треугольников OAC и OBC.
Средний геь
2. Отрезок AB проходит
через середину O отрезка CD так, что 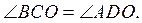 Найдите
Найдите 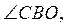 если
если 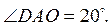
Достаточный геь
3. В треугольнике 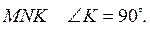 Расстояние от
точки N до прямой KM равна 5 см, а от точки M до прямой KN - 12 см. Найдите длину стороны MN, если периметр треугольника равен 30 см.
Расстояние от
точки N до прямой KM равна 5 см, а от точки M до прямой KN - 12 см. Найдите длину стороны MN, если периметр треугольника равен 30 см.
Высокий уровень
4. В треугольнике ABC
AB = BC. На сторонах AB и CB соответственно выбраны точки A1 и C1
так, что 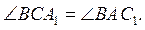 Докажите,
что
Докажите,
что 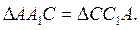
III. Мотивация
учебной деятельности. Формулировка цели и задач урока
Поскольку треугольник
и его виды по сторонами и углами рассматривались в 5 классе, желательно обратиться к
знаний учащихся и, активизировав эти знания, сформулировать цель и задачи урока.
IV. Актуализация
опорных знаний
Выполнение
устных упражнений
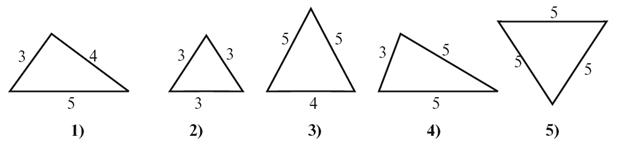
Среди треугольников
с указанными длинами сторон (рис. 1) выберите один лишний. Объясните свой
выбор.
V. Усвоение новых
знаний
План изучения
нового материала
1°. Определение
равнобедренного треугольника. Его элементы. Периметр равнобедренного треугольника.
2°. Равносторонний
треугольник как особый случай равнобедренного треугольника. Периметр
равностороннего треугольника.
3°. Теорема о
свойство углов равнобедренного треугольника и ее доведения.
4°. Следствие из теоремы
про углы равнобедренного треугольника.
VI. Первичное осознание
нового материала
Выполнение
устных упражнений
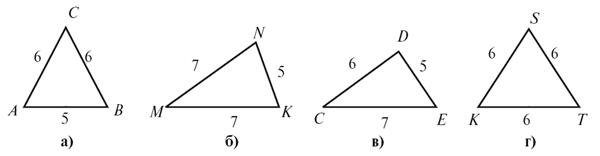
1. Какие из треугольников,
изображенных на рисунке 2, является равнобедренного? 2. Для равнобедренных треугольников,
изображенных на рисунке 2, назовите основания и боковые стороны. Вычислите периметр
каждого из равнобедренных треугольников (удобным способом).
3.
Найдите
периметр равнобедренного треугольника, если:
а) боковая сторона
равна 6 см, а основание в 3 раза меньше;
б) основание равно a
см, а боковая сторона на 2 см больше за основу.
4. В треугольнике DEF
DE = EF. Назовите равные углы треугольника.
5. Треугольник ABC -
равнобедренный с основанием AC, 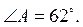 Чему равен угол С?
Чему равен угол С?
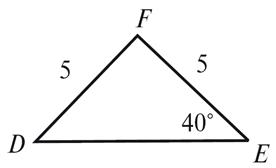
6.
Почему
равен угол D треугольника DEF, изображенного на рисунке 3?
Выполнение
письменных упражнений
Уровень А
1. Периметр
равнобедренного треугольника равна 2,6 м. Найдите стороны треугольника, если его основание больше боковой стороны на 0,2 м.
2. Если боковая сторона
и угол, противоположный основе одного равнобедренного треугольника соответственно
равны боковой стороне и углу, противоположном основе, другого равнобедренного
треугольника, то такие треугольники равны. Докажите.
Уровень Б
Периметр
равнобедренного треугольника равна 21 м. Найдите стороны треугольника, если одна
из них больше другой на 3 м. Сколько решений имеет задача?
VII. Итог урока
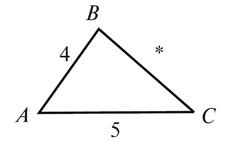
Какое число можно
поставить вместо *, чтобы Δ ABC был равнобедренным:
а) с основанием AB; б)
с основанием AC? Для каждого случая запишите равные углы (рис. 4).
VIII. Домашнее задание
Устно выполнить
упражнения.
1. Является равнобедренным
любой равносторонний треугольник? Является равносторонним любой равнобедренный
треугольник?
2. В треугольнике DEF DE
= EF. Назовите равные углы треугольника.
Письменно
решить задачи.
1. Периметр
равнобедренного треугольника равна 20 см. Найдите:
а) основу
треугольника, если его боковая сторона равна 7,5 см;
б) боковую сторону
треугольника, если его основание равно 4 см;
в) стороны
треугольника, если его боковая сторона относится к основанию как 3 : 4.
2. Если основание и угол,
прилегающий к основанию, одного равнобедренного треугольника соответственно равны
основе и углу, прилегающем к основанию, другого равнобедренного треугольника, то такие
треугольники равны. Докажите.
3. Периметр
равнобедренного треугольника ABC равна 18 см, причем основание AC меньше боковую сторону на 3 см. Найдите периметр равностороннего треугольника ADC.
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.