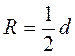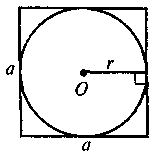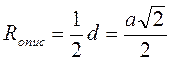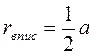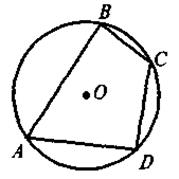
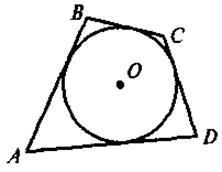
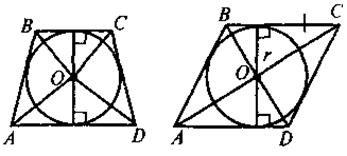
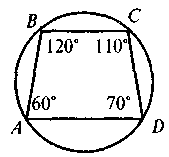
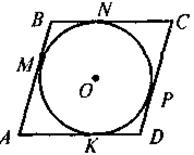
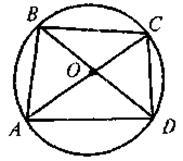
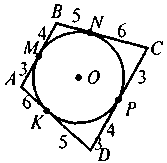
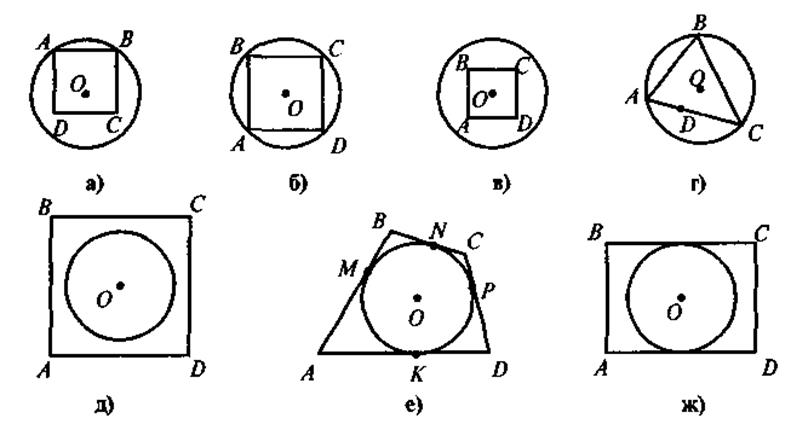
Урок № 22

Тема. Вписанные четырехугольники. Описанные четырехугольники

Цель: работать над усвоением учащимися содержания понятий: четырехугольник, вписанный в окружность; четырехугольник, описанный около окружности; рассмотреть содержание теорем о вписанный и описанный четырехугольники и схемы их доведения.

Сформировать умения:

· воспроизводить выученные утверждение;

· выполнять рисунок по описанию;

· использовать изученные теоремы при решении теоремы на четырехугольники.

Тип урока: усвоение знаний, умений и навыков.

Наглядность и оборудование: конспект «Вписанный и описанный многоугольники».

Ход урока

I. Организационный этап

II. Проверка домашнего задания

С целью экономии времени проверка домашнего задания проводится в форме беседы с готовыми рисунками (рисунки в домашних задач учитель выполняет на доске заранее; также можно записать схемы решения задач). Беседа проводится под руководством учителя, который ставит вопрос на понимание учащимися обоснование основных этапов решения задач.

III. Формулировка цели и задач урока

Учитель напоминает о составленной на 20-м уроке схему, в которой отражены логику изложения учебного материала по теме «Четырехугольники». После этого формулируется основная цель урока - изучение вопроса об определении понятия четырехугольника, вписанного в круг и описанного вокруг круга, выяснение возможностей вписать четырехугольник в окружность или описать четырехугольник вокруг круга и необходимых и достаточных условий, при которых это можно сделать.

IV. Актуализация опорных знаний

Для успешного усвоения учащимися определение, свойства, признаки и способов доказательства теорем о вписанный и описанный четырехугольники следует активизировать знания и умения учащихся относительно определения и свойства касательной к окружности и следствия из нее (свойство отрезков касательных); теоремы о бісектрису угла.

Выполнение устных упражнений по готовым рисункам

V. Усвоение знаний

План изучения материала

1. Определение четырехугольника, вписанного в круг.

2. Теорема о вписанный четырехугольник.

3. Следствия из теоремы о вписанный четырехугольник.

4. Определение описанного четырехугольника.

5. Теорема об описанный четырехугольник.

6. Следствия из теоремы об описанный четырехугольник.

@ По новой программе и математике для двенадцатилетней школы учащиеся должны не только овладеть содержанием и уметь применять в решении задач определения и теоремы о вписанный и описанный четырехугольники, а и доказывать эти теоремы. Но, учитывая достаточно высокий уровень сложности доказательства теорем, выражающих признаки вписанного и описанного четырехугольников (в учебнике этот факт зафиксирован с помощью соответствующего условного обозначения), требовать от учащихся воспроизведения доведение названных признаков автор считает нецелесообразным. Во время формирования знаний учащихся (по приведенному выше плану) учителю следует и уделю внимание таким моментам:

· во время изучения определений вписанного (описанного) четырехугольника делаем акцент на том, что только в случае, когда все вершины (стороны) четырехугольника лежат на окружности (касаются круга), данный четырехугольник будет называться вписанным в круг (описанный вокруг окружности): на этом этапе целесообразно обсудить с учащимися свойства четырехугольников и их элементов, связанные с кругом (вершины четырехугольника, вписанного в круг, равноудаленные от центра окружности; отрезок, соединяющий центр окружности с любой вершиной, является радиусом круга; для четырехугольника, описанной вокруг круга, равноудаленными от центра круга будут стороны, то есть перпендикуляр, проведенный из центра окружности, вписанной в четырехугольник, стороны четырехугольника, и является радиусом этого круга); для закрепления этих фактов предлагается выполнить задание.

Задачи. На каком из следующих рисунков изображен четырехугольник ABCD:

а) вписанный в круг;

б) описанный вокруг круга?

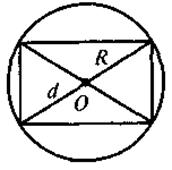
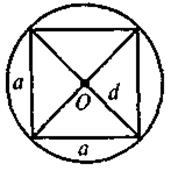
Для таких четырехугольников назовите радиусы кругов(описанного или вписанного).

· Изучив содержание теорем (которые выражают, по сути, критерии вписанного и описанного треугольников, то есть необходимое и достаточное условия) о вписан (описанный) четырехугольник, следует обратить внимание учащихся на то, что возможны два выпады их применения: во-первых, для определения того, можно ли данный четырехугольник вписать в круг (описать вокруг окружности); во-вторых, чтобы записать соответствующее соотношение для противоположных углов (сумм противоположных сторон) четырехугольника. С целью закрепления этих утверждений ученики решают устные упражнения.

Выполнение устных упражнений

1. В какой прямоугольник можно вписать окружность? Вокруг любого ромба можно описать окружность?

2. Можно ли описать окружность вокруг четырехугольника, который имеет только один прямой угол; только три прямые углы?

· Для практических нужд наибольшую ценность имеют следствия из теорем о вписанный и описанный четырехугольники, а также опорные задачи.

Задача 1. Центр окружности, описанной вокруг прямоугольника, является точкой пересечения его диагоналей.

Задача 2. Центр круга, вписанного в ромб, является точкой пересечения его диагоналей, а радиус круга равен половине высоты ромба.

Задача 3. Радиус круга, вписанного в трапецию, равен половине ее высоты.

Итак, после определения видов четырехугольников, которые можно вписать или описать, необходимо рассмотреть вопрос о положение центра описанной (вписанной) окружности и соотношение между элементами (сторонами, высотами) четырехугольников и радиусом описанной (вписанной) окружности. Соответствующие записи учащиеся должны сделать в тетрадях.

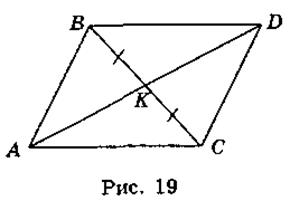
VI. Формирование первичных умений

Выполнение устных упражнений

1. Можно ли описать круг вокруг прямоугольной трапеции?

2. В трапеции три стороны равны. Можно ли в такую трапецию вписать круг? Можно ли вокруг такой трапеции описать окружность?

Выполнение письменных упражнений

1. Определите, можно ли описать окружность вокруг четырехугольника ABCD, если углы А, В, С, D равны соответственно:

а) 90°, 90°, 20°, 160°; б) 5°, 120°, 175°, 60°.

2. Найдите неизвестные углы:

а) вписанного четырехугольника, если два из них равны 46° и 125°;

б) вписанной трапеции, если один из них равен 80°;

в) вписанного четырехугольника, диагонали которого точкой пересечения делятся пополам.

3. Найдите периметр:

а) описанного четырехугольника, три последовательные стороны которого равны 7 см, 9 см и 8 см;

б) описанной трапеции, боковые стороны которой равны 3 см и 11 см.

4. Рівнобедрена трапеция описана вокруг окружности. Найдите среднюю линию трапеции, если ее боковая сторона равна 7 см.

5. Диагональ ромба, выходящий из вершины угла 60°, равна 24 см. Найдите радиус круга, вписанного в ромб.

VII. Итоги урока

Усвоение учащимися содержания основных утверждений проверяем во время Выполнения задания.

Какие ошибки допущены в изображении четырехугольников (см. рис)?

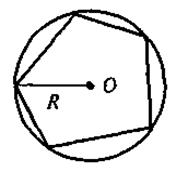
VIII. Домашнее задание

Изучить содержание теоретического материала. Выполнить домашнюю самостоятельную работу.

Домашняя самостоятельная работа

1. В треугольнике ABC точки М и N - середины сторон АВ и ВС соответственно. Периметр треугольника ABC равен 22 см. Найдите периметр треугольника MBN.

2. На рисунке ABB1 + A1AB = 180°. Найдите периметр четырехугольника АВВ1А1.

3. Найдите углы равнобедренного треугольника, основание которого взимает пятую часть дуги описанной окружности. Рассмотрите все возможные случаи.
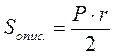