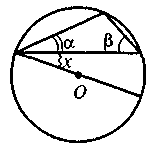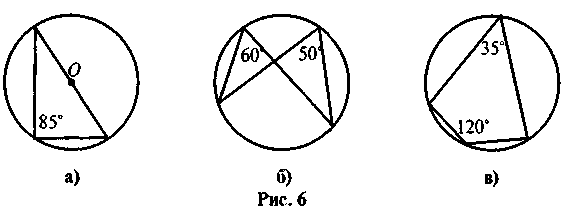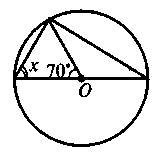Урок № 21
Тема. Следствия из теоремы о вписанный угол. Решение задач
Цель: добиться усвоения учащимися содержания следствий из теоремы о вписанный угол и способов их доказывания. Сформировать умения:
· воспроизводить содержание изученных утверждений;
· находить на рисунке объекты, свойства которых описывается этими последствиями;
· использовать изученные утверждения при решении задач на вычисление углов в круге.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Углы в окружности».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Проверку освоения учащимися способов действий, изученных на предыдущих уроках, можно провести в форме самостоятельной работы.
Самостоятельная работа
Вариант 1
1. Вершины треугольника АВС делят окружность в отношении 2:3:4. Найдите углы этого треугольника.
2. По рисунку найдите угол х (О - центр круга), α = 21°, β = 49°.
Вариант 2
1. Вершины треугольника АВС делят окружность в отношении 1:3:5. Найдите углы этого треугольника.
2. По рисунку найдите угол х (О - центр круга), α = 19°, β = 47°.
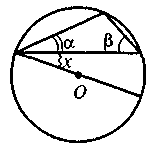
III. Формулировка цели и задач урока
Задача. Три футболиста пробивают штрафные удары по воротам из точек А, В и С (рис. 1). У кого из них угол обстрела ворот наибольший?
Во время обсуждения решения задачи необходимо перейти к ее математической модели и сформулировать проблему (как сравнить вписанные углы, опирающиеся на одну и ту же дугу?)
Понятно, что решение этой проблемы в виде некоторого правильного утверждения для вписанных углов с последующим доведением этого утверждения, а также овладение способами применения этого утверждения и является основной целью урока.
IV. Актуализация опорных знаний
Фронтальная беседа
1. Вершина угла лежит на окружности. Или обязательно этот угол является вписанным в окружность?
2. Стороны угла пересекают окружность. Или обязательно этот угол является вписанным в окружность? Может этот угол быть центральным углом?
3. АВ и ВС - хорды окружности с центром в точке О. Что можно сказать об угол ABC и АОС? Запишите правильное равенство для градусных мер этих углов.
4. Точки А и В лежат на окружности. Вписанный угол АСВ равен 90°. Чем является хорда АВ?
V. Усвоение знаний
План изучения материала
1. Следствие 1.
2. Следствие 2.
3. Следствие 3.
4*. Дополнительные последствия. Углы в круге.
@ Содержание и последовательность изучения следствий теоремы о вписанный угол логически обусловлены: следствие 1 (о вписанные углы, опирающиеся на одну и ту же дугу) основывается непосредственно на утверждении теоремы о вписанный угол. Доказательство следствия 2 (вписанный угол, опирающийся на полуокружность) можно рассматривать как особый случай следствия 1 (когда дуга окружности имеет градусную меру 180°). Что касается следствия 3 (о-центр окружности, описанной вокруг прямоугольного треугольника, и длину медианы прямоугольного треугольника, проведенной к гипотенузы), то доказательства этого утверждения становится очевидным при рассмотрении рисунка в последствии 2 (см. рис. 64 учебника). После доведения следствия 3 желательно рассмотреть интересный факт для прямоугольного треугольника (медиана прямоугольного треугольника, проведенная к гипотенузу, делит прямой угол на углы, равные острым углам прямоугольного треугольника), который желательно зафиксировать в тетрадях учащихся как опорный факт. Содержание основных следствий из теоремы о вписанный угол содержится в конспекте «Углы в окружности».
Конспект 9 |
Углы в круге |
|
|
 AOB - центральный угол, AOB - центральный угол,
 AOB = AOB = 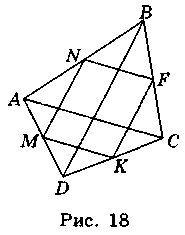 АВ АВ
Центральный угол измеряется дугой, на которую он опирается |
 ABC - вписанный угол, ABC - вписанный угол,
 ABC = ABC = 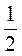  AC = AC = 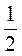  AOC AOC
Вписанный угол измеряется половиной дуги, на которую он опирается, и равен половине центрального угла, опирающегося на ту же дугу |
|
|
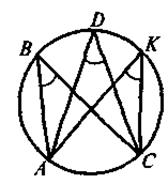
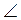 ABC = ABC = 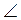 ADC = ADC = 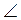 AKC AKC
Вписанные углы, опирающиеся на одну и ту же дугу, равны между собой |
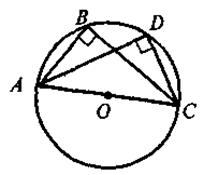
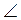 ABC = ABC = 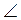 ADC = 90° ADC = 90°
Вписанный угол, опирающийся на диаметр, равен 90° |
|
|
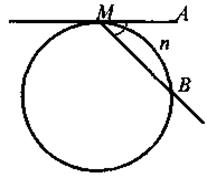
MA - касательная, MB - секущая
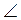 AMB = AMB = 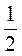 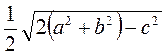 MnB MnB
|
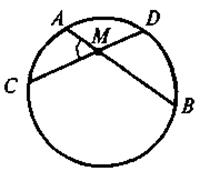
AB и CD - хорды
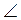 AMC = AMC = 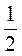 ( (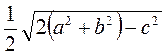 AC + AC + 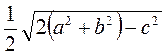 DB) DB)
|
VI. Формирование первичных умений
Выполнение устных упражнений
1. Могут ли два вписанные углы равны друг другу, если они не опираются на одну дугу?
2. Могут ли вписанные углы ABC и АВ, С не равны друг другу? Приведите пример.
3. Или может: а) угол, стороны которого пересекают окружность в концах диаметра, быть острым; б) угол с вершиной на окружности, стороны которого пересекают окружность в концах диаметра, быть острым?
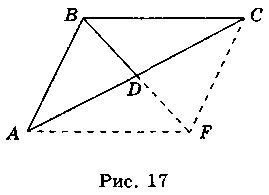
4. Дано: АВ - диаметр, АС = AD (рис. 2). Докажите, что 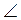 1 =
1 = 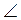 2.
2.
5. Дано: АВ - диаметр, АС - хорда (рис. 3). Докажите, что 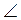 BOC = 2
BOC = 2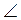 BAC.
BAC.
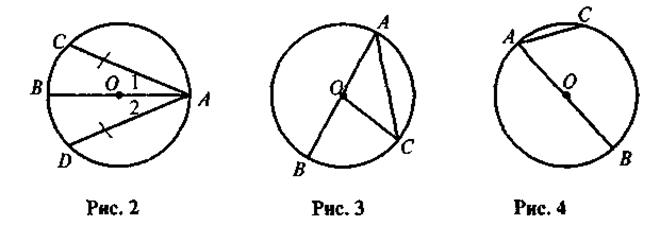
6. Дано: О - центр окружности, АС = АО (рис. 4). Найдите угол ВАС.
Выполнение письменных упражнений
1. Треугольник ABC вписан в окружность, центр которой лежит на отрезке АВ. а) Найдите угол В, если 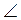 A = 65°. б) Найдите медиану, проведенную из вершины С, если АВ = 12 см.
A = 65°. б) Найдите медиану, проведенную из вершины С, если АВ = 12 см.
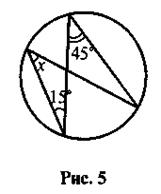
2. По данным рисунка 5 найдите угол х (точка О - центр круга).
3. На окружности отмечены точки А, В и С, причем АС - диаметр окружности,  BCA = 60°, ВС = 4 см. Найдите радиус круга.
BCA = 60°, ВС = 4 см. Найдите радиус круга.
4* (опорная). Угол между хордой и касательной к окружности, проведенной через конец хорды, измеряется половиной дуги, которая лежит внутри этого угла. Докажите.
5* (опорная), а) Дуги окружности, которые помещаются между двумя параллельными хордами, равны. Докажите, б) Равные хорды стягивают дуги с одинаковой градусной мере и наоборот: дуги с одинаковой градусной мере стягиваются равными хордами. Докажите.
VII. Итоги урока
Найдите на рисунке 6 ошибки.
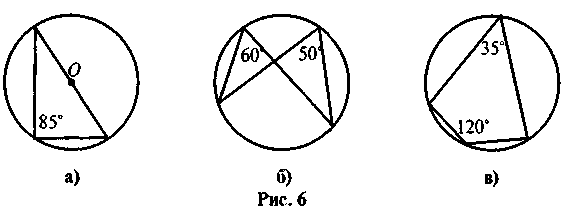
VIII. Домашнее задание
Изучить содержание последствий. Решить задачи.
1. Гипотенуза прямоугольного треугольника равна 10. Может высота, проведенная к ней, равна 6? Ответ обоснуйте.
2. По данным рисунка найдите угол х (точка О - центр круга).
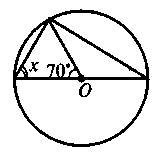
3. Найдите меньший катет прямоугольного треугольника, если его медиана равна 9 см и образует с гипотенузой угол 60°.