УРОК 22
Тема. Решение простейших тригонометрических уравнений. Уравнения tg t = a.
Цель урока: зсвоєння учащимися вывода и применения формул для нахождения корней уравнения tg t = a (ctg t = а).
Оборудование: Таблица «Уравнения tg t = а и ctg t = a».
И. Проверка домашнего задания
1. Проверить наличие домашних заданий в тетрадях учащихся. Сверить решение № 1 (8; 18) по записям на доске.
Математический диктант
Запишите решения уравнений:
1) sin x = 0; 2) sin x = 1; 3) sin x = -1; 4) sin2x = 0; 5)sin x = 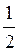 ; 6) sin x = -
; 6) sin x = -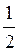 ; 7) cos x = 0; 8) cos x = 1; 9) cos x = -1; 10) cos
; 7) cos x = 0; 8) cos x = 1; 9) cos x = -1; 10) cos 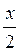 = 1; 11) cos x =
= 1; 11) cos x = 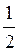 ; 12) cos x =-
; 12) cos x =-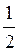 .
.
Ответ: 1) πn, n Z; 2)
Z; 2)  +2πn, n
+2πn, n Z; 3) -
Z; 3) - +2πn, n
+2πn, n Z; 4)
Z; 4) 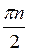 , n
, n Z; 5) (-1)n+1
Z; 5) (-1)n+1 + πn, n
+ πn, n Z; 6) (-1)n+1
Z; 6) (-1)n+1 + πn, n
+ πn, n Z;
Z;
7)  + πn, n
+ πn, n Z; 8) 2πn, n
Z; 8) 2πn, n Z; 9) n + 2πn, n
Z; 9) n + 2πn, n Z; 10) 4πn, n
Z; 10) 4πn, n Z; 11) ±
Z; 11) ± + 2πn, n
+ 2πn, n Z; 12) ±
Z; 12) ±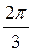 + 2πn, n
+ 2πn, n Z.
Z.
II. Сообщение темы урока
III. Восприятия и осознания материала о решения уравнения tg t = a (ctg t = a)
Демонстрируется таблица 10.
Таблица 10
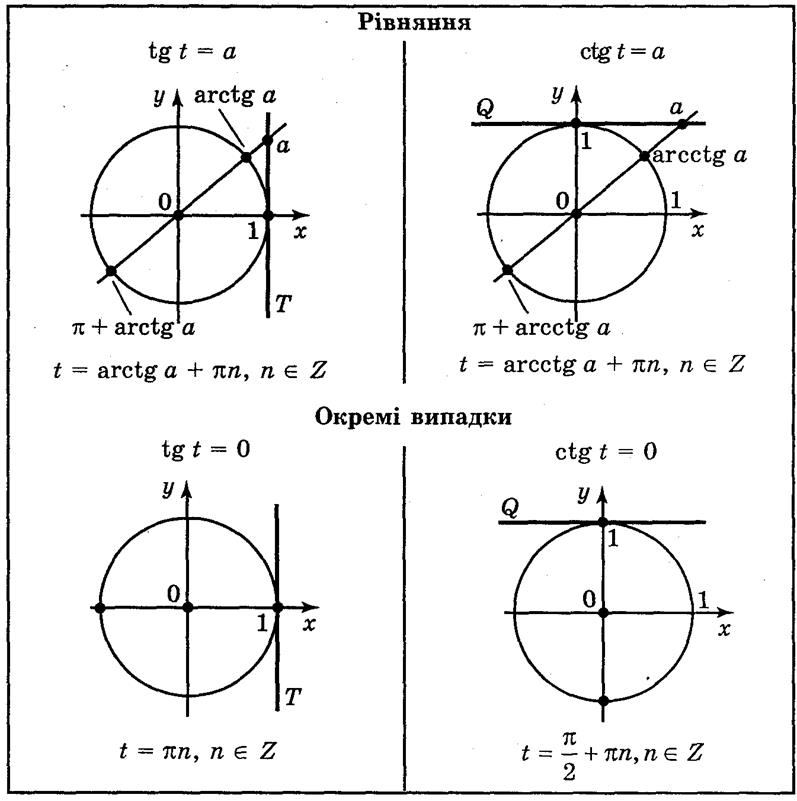
Объяснение учителя
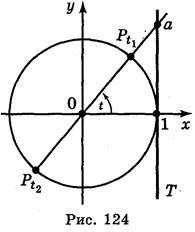
Решения уравнения tg t = а удобно проиллюстрировать с помощью линии тангенсов (рис. 124). tg t - это ордината точки пересечения прямой ОРt с линией тангенсов. Отложим на оси тангенсов число а, через эту точку и начало координат проведем прямую, которая пересечет единичный круг в двух точках 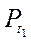 и
и 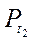 , тогда
, тогда
t = arctg a + πn, n Z (1)
Z (1)
Следовательно, уравнение tg t = а при любом значении а имеет решение.
Уравнения ctg t = а, где а ≠ 0 равносильно уравнению tg t = 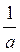 .
.
Однако можно доказать, что решение уравнения ctg t = а можно записать в виде:
t = arcctg a + πп, n Z (2)
Z (2)
Рассмотрим примеры.
Пример 1. Решите уравнение tg x =  .
.
Решение
По формуле (1) находим х = arctg  + πn, n
+ πn, n Z.
Z.
Поскольку arctg  =
=  , то имеем: х =
, то имеем: х =  + πn, n
+ πn, n Z.
Z.
Ответ:  + πn, n
+ πn, n Z.
Z.
Пример 2. Решите уравнение tg х = 2.
Решение
По формуле (1) имеем: х = arctg 2 + πn, n Z. Значение arctg 2 можно найти с помощью микрокалькулятора arctg2
Z. Значение arctg 2 можно найти с помощью микрокалькулятора arctg2 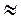 1,1, тогда х
1,1, тогда х 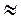 1,1 + πn, n
1,1 + πn, n Z.
Z.
Ответ: arctg 2 + πn 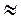 1,1 + πn, n
1,1 + πn, n Z.
Z.
Пример 3. Решите уравнение ctg x -  = 0.
= 0.
Решение
ctg х -  = 0; ctg х =
= 0; ctg х =  ; tg х =
; tg х = 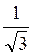 , x = arctg
, x = arctg 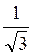 + πn =
+ πn =  + πn, n
+ πn, n Z.
Z.
Ответ:  + πn, n
+ πn, n Z.
Z.
IV. Осмысление изученного материала
Выполнение упражнений_____________________________
Решите уравнение.
1. a) tg x +  = 0; б) ctg x + 1 = 0; в)
= 0; б) ctg x + 1 = 0; в)  tg x - 1 = 0; г)
tg x - 1 = 0; г)  ctg x - 1= 0.
ctg x - 1= 0.
Ответ: а) -  + πn, n
+ πn, n Z; б)
Z; б) 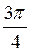 + πn, n
+ πn, n Z; в)
Z; в)  + πn, n
+ πn, n Z; г)
Z; г)  + πn, n
+ πn, n Z.
Z.
2. а) 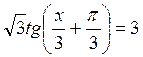 ; б)
; б) 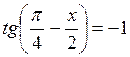 .
.
Ответ: а) 3 πn, n Z ; б) n + 2 πn, n
Z ; б) n + 2 πn, n Z.
Z.
3. a) 3tg2 x + 2 tg x - 1 = 0;
б) 2ctg2 x + 3ctg x - 2 = 0;
в) tg x - 2ctg x + 1 = 0;
г)  tg2 x - 3tg x = 0.
tg2 x - 3tg x = 0.
Ответ: а) - + πn и arctg
+ πn и arctg 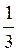 + πn, n
+ πn, n Z;
Z;
б) arctg 2 + πn и-arctg 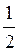 + πn, n
+ πn, n Z;
Z;
в)  + πn и-arctg 2 + πn, n
+ πn и-arctg 2 + πn, n Z;
Z;
г) πn и  + πn, n
+ πn, n Z.
Z.
V. Подведение итогов урока
VI. Домашнее задание
Раздел II § 2 (3). Вопросы и задания для повторения раздела II № 13-15. Упражнение№ 1 (4; 11; 12; 15; 16).