УРОК 21
Тема. Решение простейших тригонометрических уравнений. Уравнения sin t = а
Цель урока: усвоение учащимися вывода и применения формул для корней уравнения sin t = а.
Оборудование: Таблица «Уравнения sin t = а».
И. Проверка домашнего задания
1. Ответы на вопросы, возникшие при выполнении домашних заданий.
2. Самостоятельная работа.
Вариант 1
Решите уравнение:
а) 2cos 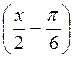 =
=  . (3 балла)
. (3 балла)
б) 2cos2x + cos x - 1 = 0. (3 балла)
в) 4cos x = 4 - sin x. (3 балла)
г) sin 3x sin x - cos 3x cos x = 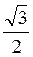 . (3 балла)
. (3 балла)
Вариант 2
Решите уравнение :
а) 2 cos 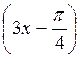 =
= 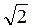 . (3 балла)
. (3 балла)
б) 2cos2x - cosx - 1 = 0. (3 балла)
в) 8 sin2х + cosx + 1 = 0. (3 балла)
г) sin2 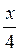 - cos2
- cos2 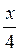 = 1. (3 балла)
= 1. (3 балла)
Ответ:
B-1. a) ±
± +4πn, n
+4πn, n Z; б) ±
Z; б) ± +2πn и π+2πn, n
+2πn и π+2πn, n Z; в)2πn, n
Z; в)2πn, n Z; г) ±
Z; г) ±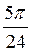 +πn,n
+πn,n Z.
Z.
В-2. a) 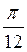 ±
±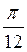 +
+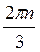 , n
, n Z; б) 2πn и ±
Z; б) 2πn и ±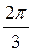 +2πn, n
+2πn, n Z; в) n+2πn, n
Z; в) n+2πn, n Z; г) 4πn, n
Z; г) 4πn, n Z.
Z.
II. Сообщение темы урока
III. Восприятия и осознания материала о решения уравнения sin t = a
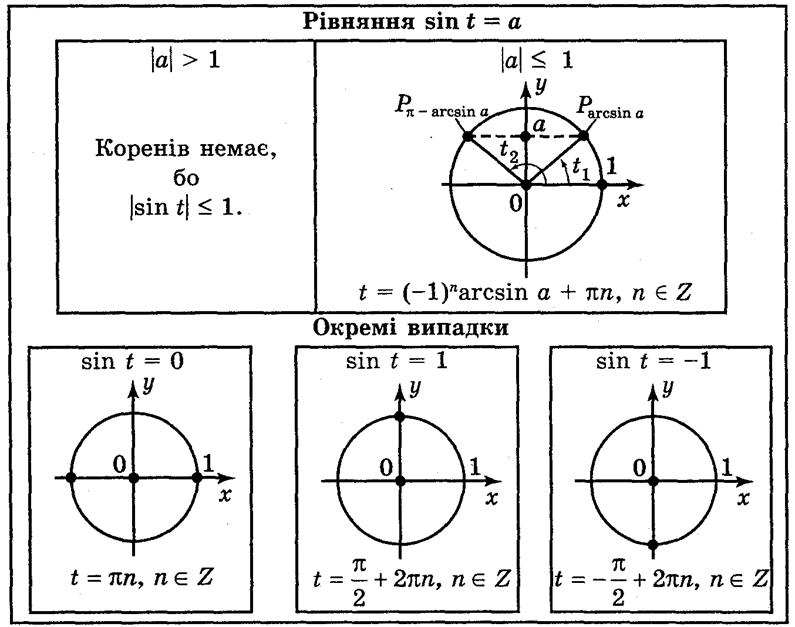
Демонстрируется таблица 9.
Объяснение учителя
1) Если |а| > 1, то уравнение не имеет решений, поскольку |sin x| 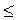 1 для любого t.
1 для любого t.
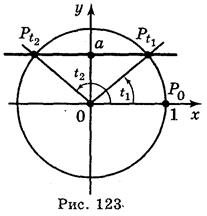
2) Если |а| 1, то, учитывая, что sin t - ордината точки Рt единичного круга, имеем: ординату, равную а, имеют две точки единичного круга (на оси OY откладываем число а и через эту точку проведем прямую, перпендикулярную оси ординат (рис. 123), которая пересечет окружность в двух токах - 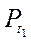 и
и 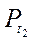 ):
):
t1 = arcsin a + 2πn, n Z,
Z,
t2 = n - arcsin а + 2πn, n Z.
Z.
Эти две формулы можно записать в виде одной формулы:
t = (-1)k arcsin a + nk, k Z (1)
Z (1)
Нетрудно убедиться, что при парном k = 2π имеем:
t1 = (-1)2n arcsin а + 2πn или t1 = arcsin a + 2πn, n Z;
Z;
при нечетном k = 2n + 1 имеем:
t2 = (-1)2n+1 arcsin а + (2n + 1)n;
t2 = - arcsin а + 2πn + n;
t2 = n - arcsin a + 2πn, n Z.
Z.
3) Если а = 1, то, учитывая то, что sint - это ордината точки Pt (единичного круга, имеем: ординату, равную 1, точка Рt образована из точки Р0(1;0) поворотом на угол  + 2πn, n
+ 2πn, n Z.
Z.
Следовательно, t =  + 2πn, n
+ 2πn, n Z. Если а = -1, то t = -
Z. Если а = -1, то t = - + 2πn, n
+ 2πn, n Z.
Z.
4) Если а = 0, имеем t = 0 + πn; t = πn, n Z.
Z.
Рассмотрим примеры.
Пример 1. Решите уравнение sinx = 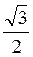 .
.
Решение
Согласно формуле (1) имеем: х = (-1)n arcsin 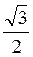 + πn, n
+ πn, n Z.
Z.
Поскольку arcsin 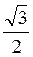 =
=  , то х = (-1)n
, то х = (-1)n  + πn, n
+ πn, n Z.
Z.
Ответ: (-1)n  + πn, n
+ πn, n Z.
Z.
Пример 2. Решите уравнение sin х = - 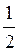 .
.
Решение
Согласно формуле (1) имеем: х = (-1)n arcsin 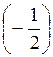 + πn, n
+ πn, n Z.
Z.
Поскольку arcsin 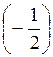 = -
= -  , то х =(-1)n ·
, то х =(-1)n ·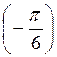 + πn, n
+ πn, n Z; х = (-1)n+1 + πn, n
Z; х = (-1)n+1 + πn, n Z.
Z.
Ответ: (-1)n+1 + πn, n Z.
Z.
Пример 3. Решите уравнение sin x = 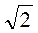 - 1.
- 1.
Решение
Согласно формуле (1) имеем: х = (-1)n arcsin(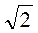 - 1) + πn, n
- 1) + πn, n Z.
Z.
Значение arcsin(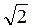 -1) найдем с помощью микрокалькулятора:
-1) найдем с помощью микрокалькулятора:
arcsin(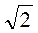 - 1)
- 1) 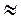 0,427, тогда х
0,427, тогда х 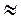 (-1)n · 0,427 + πn, n
(-1)n · 0,427 + πn, n Z.
Z.
Ответ: (-1)n · arcsin(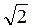 -1) + πn
-1) + πn 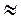 (-1)n · 0,427 + πn, n
(-1)n · 0,427 + πn, n Z.
Z.
IV. Осмысление изученного материала
Комментируемое выполнения упражнений
Решите уравнение.
1. a) 2sin x - 1 = 0; б) 2sin 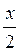 = - 1; в) 2sin
= - 1; в) 2sin 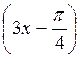 = -
= - 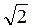 ; г) 2sin
; г) 2sin 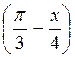 =
=  .
.
Ответ: а) (-1)n + πn, n
+ πn, n Z; б) (-1)n+1
Z; б) (-1)n+1 + 2πn, n
+ 2πn, n Z; в)
Z; в) 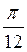 +(-1) n+1
+(-1) n+1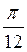 +
+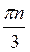 , n
, n Z; г)
Z; г) 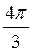 +(-1)n+1
+(-1)n+1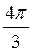 + 4πn, n
+ 4πn, n Z.
Z.
2. a) sin 3x cos x - cos 3x sin х = 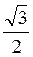 ;
;
б) sin 2x cos 2x = - 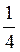 ;
;
в) sin 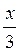 cos
cos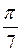 - cos
- cos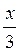 sin
sin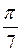 =
= 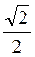 ;
;
г) cos 2x sin 3x + sin 2x cos 3x = 1.
Ответ: а) (-1)n +
+ 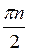 , n
, n Z; б) (-1)n+1
Z; б) (-1)n+1 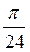 +
+ 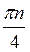 , n
, n Z; в)
Z; в) 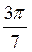 (-1)n
(-1)n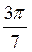 +3 πn, n
+3 πn, n Z; г)
Z; г) 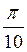 +
+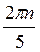 , n
, n Z.
Z.
3. а) (2sin x - 1)(3sin x + 1) = 0; б) (4sin 3х - 1)(2sin х + 3) = 0.
Ответ: а) (-1)n + πn и (-1)n+1arcsin
+ πn и (-1)n+1arcsin 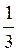 + πn, n
+ πn, n Z; б) (-1)n
Z; б) (-1)n 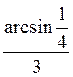 +
+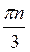 , n
, n Z.
Z.
Таблица 9
V. Подведение итогов урока
VI. Домашнее задание
Раздел II § 2 (1). Вопросы и задания для повторения раздела II № 13-15. Упражнения№ 1 (6; 7; 8; 14; 17; 18), № 2 (3).