Урок № 20

Тема. Градусная мера дуги. Вписанный угол

Цель: добиться усвоения учащимися содержания понятий: плоский угол (в неявном виде), центральный угол, дуга окружности, соответствующей данному центральному углу, градусная мера дуги окружности, вписанный угол, - а также усвоения учащимися содержания свойства вписанного угла (об измерении вписанного угла).

Формировать умения:

· воспроизводить содержание изученных утверждений;

· находить на готовом рисунке изученные понятия;

· выполнять правильные изображение изученных понятий заданным описанием;

· решать задачи с использованием изученных утверждений на вычисление градусной меры вписанных и центральных углов.

Тип урока: применение знаний, умений и навыков.

Наглядность и оборудование: схема.

Ход урока

I. Организационный момент

II. Проверка домашнего задания

Проверка правильности выполнения письменной части домашнего задания происходит во время проверки тетрадей с выполненной домашней самостоятельной работой. На уроке для обратной связи учитель лишь объявляет правильные ответы (при необходимости выдает ученикам правильные решения для выполнения работы над ошибками дома).

III. Формулировка цели и задач урока

Для понимания логики изучения материала (как это правильно замечают авторы учебника) можно обратиться к логической схемы построения курса геометрии 7 класса, а потом составить соответствующую схему для отображения логики изучения материала в 8 классе. Результат может иметь следующий вид (см. схему).

Схема

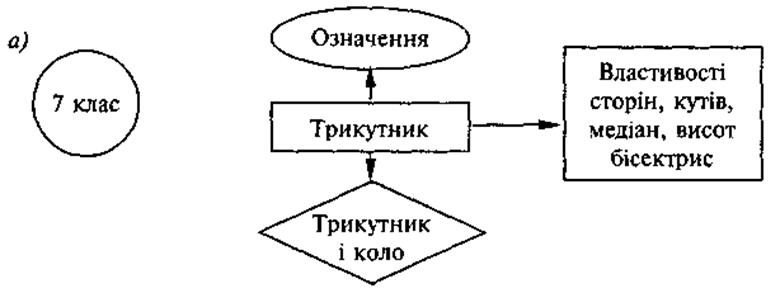
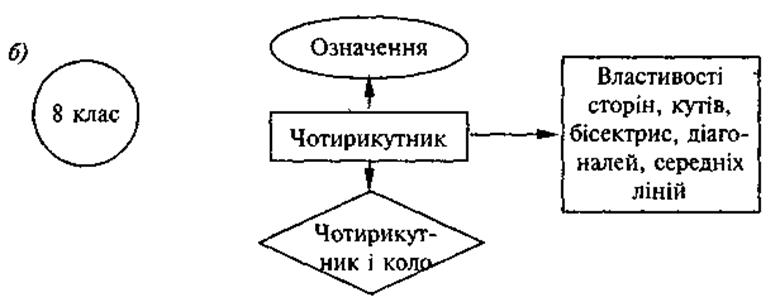
После осознание учащимися логики изучения материала на следующие три урока, учитель должен объяснить, что для изучения случаев взаимного расположения четырехугольника относительно круга необходимые знания дополнительного материала (без его понимания невозможно изучение понятия четырехугольника, вписанного и описанного вокруг круга).

Итак, целью урока как раз и является изучение понятий, связанных с углами в кругу, а также исследование способов их применения на практике.

IV. Актуализация опорных знаний

Для сознательного усвоения учащимися определение, свойства и способа доведения свойства центрального и вписанного кругов следует активизировать знания и умения учащихся по определению круга и свойств точек, принадлежащих окружности; определение угла и свойств измерения углов; определение и свойства внешнего угла треугольника; понятие круга, описанного вокруг треугольника и его свойств.

Выполнение устных упражнений

1. Продолжим все радиусы кругов на одну и ту же длину (в сторону, противоположную относительно центра). Какую линию образуют их концы? Ответ объясните.

2. О - центр окружности, АВ = ВС (рис. 1). Докажите, что 1 = 2.

3. Назовите на рисунке 2 наибольший угол.

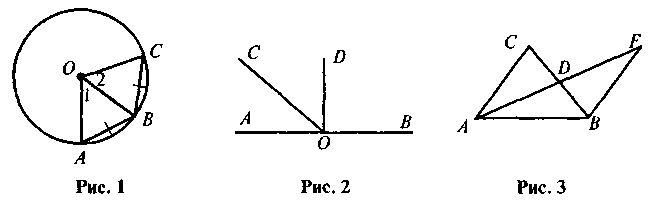
4. Назовите треугольники, для которых CDF является внешним (рис. 3); BDF является внешним.

5. В треугольнике ABC центр описанной окружности лежит на медиане AD. Что можно сказать про этот треугольник?

V. Усвоение умений и навыков

План изучения нового материала

1. Расширение понятия угла.

2. Центральный угол: определение, измерение.

3. Градусная мера дуги.

4. Определение вписанного угла. Дуга, на которую опирается вписанный угол.

5. Теорема о вписанный угол: формулировка и доказательство.

@ Изучения вопроса об углы в круге за новым учебником ведется традиционным способом (см. План изучения нового материала). Это касается определений понятий «центральный угол», «дуга окружности, соответствующей данному центральному углу», «градусная мера дуги окружности», «вписанный угол», а также формулировки и способа доказательства теоремы о вписанный угол. Но, в отличие от традиционного учебника, авторы нового пособия избегают использовать понятие плоского угла, заменив его на понятие угла, который может иметь градусную меру, что превышает 180° (то есть понятие плоского угла дается на интуитивном уровне). Также авторы избегают понятия «доповняльні плоские углы» (хотя неявно оговаривают, что угол делит плоскость на две части, то есть декларируется существование двух углов на рис. 58 учебника). Поэтому во время изучения нового материала, чтобы избежать путаницы в понятиях учеников, учителю сразу следует объяснить, что на уроке речь идет об углы как части плоскости, а потому в отличие от углов как геометрических фигур, состоящих из двух лучей, выходящих из одной точки, названные углы будут иметь некоторые особые свойства (например, могут иметь градусную меру, большую на 180°).

Дальнейшее изучение материала урока проводится согласно учебника по записанным выше плану.

Выполнение устных упражнений

1. На каждом из рисунков найдите и назовите:

а) центральный угол;

б) дугу, что соответствует центральном кугу;

в) вписанный угол, опирающийся на эту дугу.

2. Определите, есть вписанный угол ABC острым, прямым или тупым, если:

а) дуга ABC меньше полукруга;

б) дуга ABC больше полукруг;

в) дуга ABC равна полуокружности.

3. Сторона вписанного угла проходит через центр окружности. Или может быть угол тупой; прямым?

Выполнение графических упражнений

1. Начертите круг с центром и отметьте на нем точки А, В и С.

а) Выделите двумя цветами доповняльні плоские углы, образованные лучами ОА и ОС.

б) Каким цветом выделен угол, вдвое больший угол ABC?

в) Отметьте на окружности точку D так, чтобы вписанные углы ABC и ADC были равны.

Выполнение письменных упражнений

1. Найдите доповняльні плоские углы, если:

а) один из них больше другого на 120°;

б) их градусные меры относятся как 2:7.

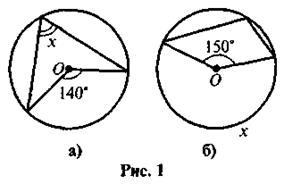
2. По данным рисунка 1 найдите градусную меру х (точка О - центр круга).

3. На окружности отмечены точки А, В, С и D. Найдите угол ABC, если ADC = α. Сколько решений имеет задача?

VII. Итоги урока

Найдите ошибки на рисунке 2.

VIII. Домашнее задание

Изучить содержание теоретических утверждений и доказательства теоремы о вписанный угол.

Решить задачи.

1. Найдите градусную меру дуги, которая составляет:

а) четверть круга; б) треть круга; в) 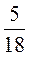круга.

2. По данным рисунка найдите градусную меру х (точка О - центр круга).

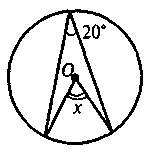
3. Хорда АС делит окружность на две дуги, градусные меры которых относятся как 11 : 7. Найдите угол ABC, если точка В лежит на большей дуге.