УРОК 20
Тема. Решение простейших тригонометрических уравнений. Уравнения cos t = a
Цель урока: усвоение учащимися вывода и применения формул для нахождения корней уравнения cos t = a.
Оборудование: Таблица «Уравнения cos t = a».
И. Проверка домашнего задания
Математический диктант
Вычислите:
1) arcsin 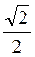 ; 2) arcos
; 2) arcos 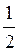 ; 3) arctg
; 3) arctg  ; 4) arcsin
; 4) arcsin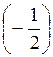 ; 5) arccos
; 5) arccos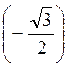 ; 6) arctg (-1);
; 6) arctg (-1);
7) arcctg (-1); 8) cos (arсcos 1); 9) sin 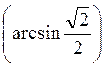 ; 10) arcsin
; 10) arcsin 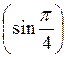 ; 11) arccos
; 11) arccos 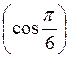 ; 12) arccos
; 12) arccos 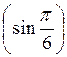 .
.
Ответы:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) -
; 4) - ; 5)
; 5)  ; 6) -
; 6) - ; 7)
; 7) 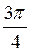 ; 8) 1; 9)
; 8) 1; 9) 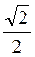 ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  .
.
II. Мотивация обучения и сообщение темы урока
Всем известно, что квадратные уравнения можно решать с помощью формулы их корней, что значительно упрощает работу.
В математике рассматривают уравнения, в которых неизвестное (сменная) входит только под знак тригонометрических функций, например: cos t = 1, cos t + sin t = 0. Эти уравнения называются тригонометрическими уравнениями. Как правило, решения любого тригонометрического уравнения сводится к решению простейших уравнений: sin t = a, cos t = a, tg t = a, ctg t = a.
Итак, наша задача - вывести формулы для решения простейших тригонометрических уравнений и научиться решать тригонометрические уравнения, приводимые к простейшим.
На сегодняшнем уроке рассмотрим решение уравнения cos t = a.
III. Восприятия и осознания материала о решения уравнения cos t = а
Демонстрируется таблица 8.
Таблица 8
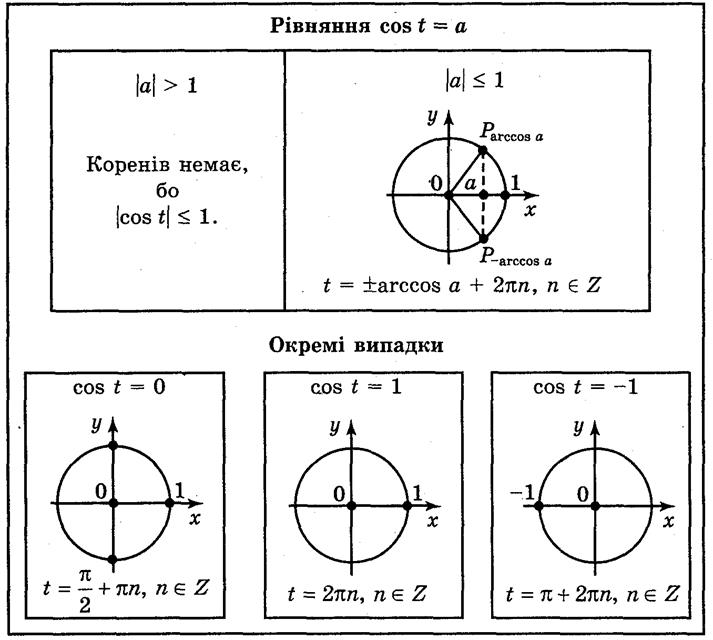
Объяснение учителя
1. Если |а| > 1, то уравнение cos t = а не имеет решений, во-сколько |cos t| 1 для любого t.
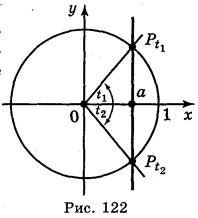
2. Если |а| 1, то учитывая, что cos t - абсцисса точки Рt единичного круга, имеем: абсцису, равную а, имеют две точки (рис. 122) единичного круга(на оси ОХ отложим число а и через построенную точку проведем прямую, перпендикулярную оси абсцисс, которая пересечет окружность в двух точках 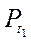 и
и  . Тогда
. Тогда
t1 = arccos a + 2πn, n Z,
Z,
t2 = - arccos a + 2πn, n Z.
Z.
Эти решения можно объединить
t = ± arccos a + 2πn, n Z (1)
Z (1)
3. Если а = 1, то, учитывая, что cos t - это абсцисса точки Рt единичного круга, имеем: абсцису, равное 1, имеет точка Рt образована из точки Р0(1; 0) поворотом на углы 2πn, n Z. Следовательно, t = 0 + 2πn = 2πn, n
Z. Следовательно, t = 0 + 2πn = 2πn, n Z.
Z.
4. Если а = -1, то имеем t = n + 2πn, n Z. Корни уравнений: cos t = 1, cos t = -1, cos t = 0 можно получить из формулы t = ± arccos a + 2πn, n
Z. Корни уравнений: cos t = 1, cos t = -1, cos t = 0 можно получить из формулы t = ± arccos a + 2πn, n Z. Рассмотрим примеры.
Z. Рассмотрим примеры.
Пример 1. Решите уравнение cos x = 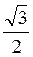 .
.
Решение
Согласно формуле (1) имеем:
х = ± arccos 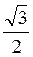 + 2πn, n
+ 2πn, n Z.
Z.
Поскольку arccos 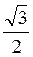 =
=  , то имеем: х = ±
, то имеем: х = ±  + 2πn, nєZ.
+ 2πn, nєZ.
Ответ: ±  + 2πn, n
+ 2πn, n Z.
Z.
Пример 2. Решите уравнение cos x = 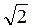 .
.
Решение
Поскольку 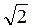 > 1, то уравнение корней не имеет.
> 1, то уравнение корней не имеет.
Ответ: корней нет.
Пример 3. Решите уравнение cos x = 0,37.
Решение
Согласно формуле (1) имеем:
х = arccos 0,37 + 2πn, n Z.
Z.
Значение arccos 0,37 найдем с помощью микрокалькулятора: arccos 0,37 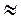 1,19, тогда х
1,19, тогда х 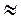 ± 1,19 + 2πn, n
± 1,19 + 2πn, n Z.
Z.
Ответ: arccos 0,37 + 2πn 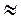 ± 1,19 + 2πn, n
± 1,19 + 2πn, n Z.
Z.
Пример 4. Решите уравнение cos x = -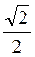 .
.
Решение
Согласно формуле (1) имеем: х = ±arccos 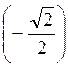 + 2πn, n
+ 2πn, n Z.
Z.
Поскольку arccos 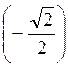 = n - arccos
= n - arccos 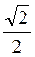 = n -
= n -  =
= 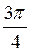 , то x = ±
, то x = ± 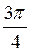 + 2πn, n
+ 2πn, n Z.
Z.
Ответ: ± 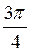 + 2πn, n
+ 2πn, n Z.
Z.
IV. Осмысление изученного материала
Выполнение упражнений______________________________
Решите уравнение.
1. a) -2cos х = 1; б) cos 2х - 1 = 0; в) 2cos 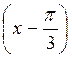 =
=  ; г)
; г) 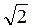 - 2cos
- 2cos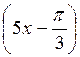 = 0.
= 0.
Ответ: а)±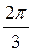 +2πn, n
+2πn, n Z; б) πn, n
Z; б) πn, n Z; в)
Z; в)  ±
± +πn, n
+πn, n Z; г)
Z; г) 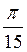 ±
± 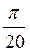 +
+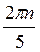 , n
, n Z.
Z.
2. a) cos x cos 3x = sin 3x sиn x;
б) cos 2x cos x + sin 2x sin х = 1;
в) cos2 x - sin2 х = 0,5;
г) 2sin2x = 1.
Ответ: а) 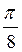 +
+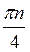 , n
, n Z; б) 2πn, n
Z; б) 2πn, n Z; в) ±
Z; в) ± +πn, n
+πn, n Z; г)
Z; г)  +
+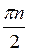 , n
, n Z.
Z.
3. а) 6соз2х + cos x - 1 = 0;
б) cos x + 3cos х = 0;
в) 4cos2x - 3 = 0;
г) cos2x = 1 + sin2x.
Ответ: а) ± 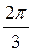 + 2πn; ± arccos
+ 2πn; ± arccos 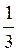 + 2πn, n
+ 2πn, n Z; б)
Z; б)  + πn, n
+ πn, n Z; в) ±
Z; в) ± + 2πn и ±
+ 2πn и ±  + 2πn, n
+ 2πn, n Z; г)
Z; г) 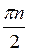 , n
, n Z.
Z.
4. а) (1 + cos x)(3 - 2cos x) = 0;
Ответ: а) n + 2πn, n Z.
Z.
V. Итог урока
VI. Домашнее задание
Раздел II § 2 (2). Вопросы и задания для повторения раздела II № 13-15. Упражнения№ 1 (9; 10; 13), № 2 (2; 4; 7).