АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§24. СИСТЕМЫ, СОДЕРЖАЩИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ.

При решении систем, содержащих тригонометрические уравнения, используют приемы решения систем (способ подстановки, способ сложения замену переменных) и методы решения тригонометрических уравнений.

Пример 1. Решите систему уравнений

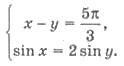
Решения. Выражая из первого уравнения х через у, имеем: 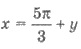и подставляя во второе, имеем

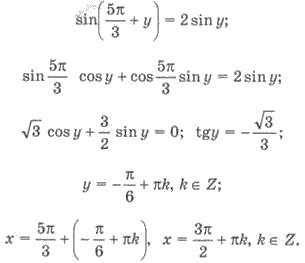
Следовательно, 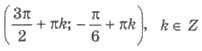- решение системы.

Пример 2. Решите систему уравнений

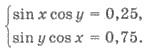
Решения. Добавим уравнения системы, имеем

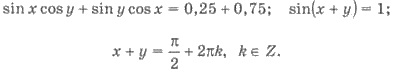
Вычитая из первого уравнения системы второе, получим

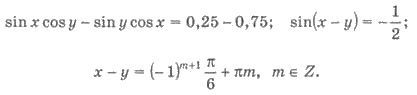
Имеем

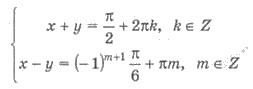
Дальше

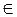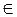где k Z; m Z.