АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§25. ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА.

Неравенства, содержащие неизвестные под знаками тригонометрических функций, называют тригонометрическими неровностями.

Примерами тригонометрических неравенствами являются неравенства

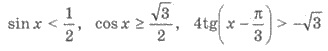т.д.

К простейшим будем относить неравенства вида 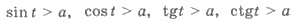и другие, у которых на месте знака > стоит один из знаков ≥, или ≤. Общие формулы для решения этих неравенств являются довольно громоздкими. Поэтому рассмотрим методы решения этих неровностей на примерах. Для наглядности будем использовать единичный круг, линии тангенса и котангенса.

Пример 1. Решить неравенство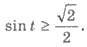

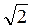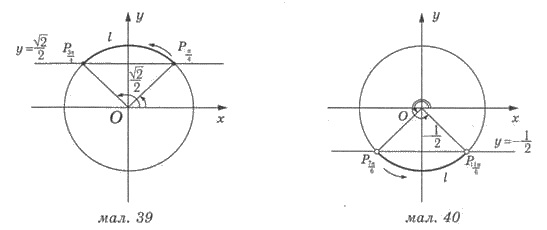
Решения. sin t - это ордината точки единичной окружности, соответствующей углу t. Сначала обозначим на единичном круге все точки, ординаты которых больше /2; эти точки находятся выше прямой у = 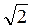/2 (рис. 39). Множество всех таких точек - дуга l. Если двигаться по этой дуге против движения часовой стрелки, то начальная точка дуги l соответствует углу аrсsin 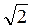/2 = π/4, а конечная - 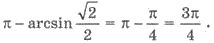Углы, соответствующие этим точкам, входят в ответ (поскольку знак неравенства ≥), а потому на рисунке обозначены точки жирно. Таким образом, неравенство sin t ≥ 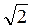/2 удовлетворяют все значения t такие, что 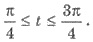Поскольку синус является функцией периодической с наименьшим положительным периодом 2π, то множество всех решений неравенства получим, добавив к чисел π/4 и 3π/4 числа вида 2πk, k 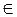Z. Итак, имеем:

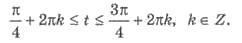
Ответ можно подать и так:

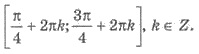
Пример 2. Решить неравенство

Решения. Обозначим 2х = t, имеем неравенство sиn t -1/2. Обозначим на единичном круге все точки, ординаты которых меньше -1/2, это точки дуги l, которые расположенные ниже прямой у = -1/2 (рис. 40). Конце этой дуги - точки, ординаты которых равны-1/2; углы, соответствующие этим точкам, не входят в ответ, поскольку знак неравенства ““. Поэтому точки на рисунке «выколоты». Если двигаться по дуге l против часовой стрелки, то начальная

точка дуги l соответствует углу 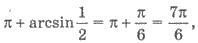a конечная - кута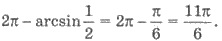

Учитывая периодичность, имеем:

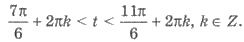
Возвращаемся к переменной х:

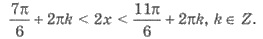
Разделим все три части двойной неравенства на 2. Имеем:

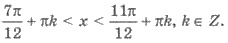
Пример 3. Решить неравенство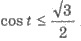

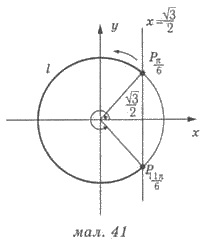
Решения. cos t - это абсцисса точки единичной окружности, соответствующей углу t. Обозначим на единичном круге все точки, абсциссы которых меньше /2, эти точки расположены левее прямой х = /2 (рис. 41), образуют дугу l. Углы, которые соответствуют крайним точкам дуги, входящие в ответ (поскольку знак неравенства ≤), поэтому точки на рисунке обозначены жирно. При движении против часовой стрелки начальная точка дуги l соответствует углу arccos /2 = π/6, а конечная - кута

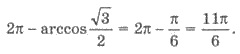
Учитывая периодичность косинуса, получим решения неравенства:

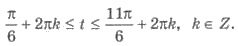
Пример 4. Решить неравенство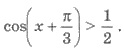

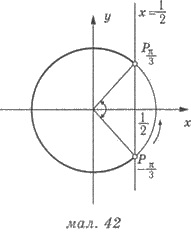
Решения. Обозначим х + π/3 = t, имеем cos t > 1/2. На рисунке 42 выделено соответствующую дугу l, ее конечная точка соответствует углу arccos 1/2 = π/3, a начальная - кута arccos 1/2 = = -π/3. Имеем:

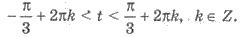
Возвращаемся к переменной х:

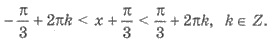
Отнимем от трех частей двойной неравенства π/3. Имеем:

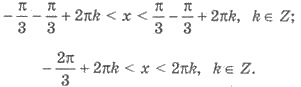
Для иллюстрации решений неровностей, в которых в левой части находится tg t, а в правой - число, ознакомимся с линией тангенсов.

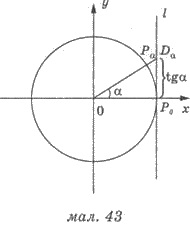
Рассмотрим прямую l, которая является касательной к единичной окружности и проходит через точку (1;0) (рис. 43). Пусть при повороте на угол α начальный радиус ОР₀ переходит в радиус ОВ_α. Пусть прямая ОР_α пересекает прямую l в точке D_α. Тогда ордината точки D_α равен тангенсу α.

Пример 5. Решить неравенство tg t ≤ .

Решения. Период функции тангенс равен π,поэтому сначала найдем решения неравенства на промежутке (-π/2;π/2), а затем используем периодичность.

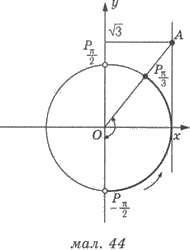
Проведем линию тангенсов, tg t - это ордината точки линии тангенсов, что соответствует углу t. Обозначим на линии тангенсов точку, ордината которой равен - точку А (рис. 44). Эта точка соответствует углу 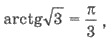а точки линии тангенсов, в которых ординаты меньше , соответствуют углам от -π/2 до π/3. Заметим, что угол π/3 будет входить в ответ (поскольку знак неравенства ≤), а угол -π/2 - не будет, поскольку tg (-π/2) - не существует. Следовательно на промежутке (-π/2;π/2) неравенство tg t ≤ имеет развязки 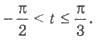Учитывая периодичность, имеем:

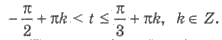
Пример 6. Решить неравенство tg t ≥ .

Решения. Используя рисунок 44 и периодичность, имеем:

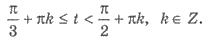
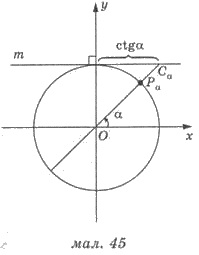
Прямую m, которая проходит через точку (0;1) перпендикулярно к оси ординат, называют линией котангенсів (рис. 45). Абсцисса точки С_α пересечения прямой ОР_α с линией котангенсів равна котангенсу α.

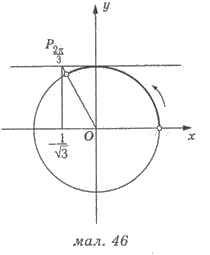
Пример 7. Решить неравенство ctg t > -1/.

Решение (рис. 46). Используя линию котангенсів, получим решение неравенства на промежутке

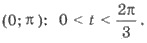
Дальше используем периодичность: