АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§23. МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.

4. Однородные тригонометрические уравнения и уравнения, сводящиеся к однородным.

Тригонометрические уравнения a sin х + b cos х = 0, где а и b - числа, а ≠ 0, b ≠ 0, называют однородными тригонометрическими уравнениями 1-й степени относительно sin х и cos х.

Те значения х, при которых cos x = 0 не являются корнями уравнения. Действительно в случае cos х = 0 уравнение принимает вид a sin x = 0. Так как а ≠ 0, то получим sin x = 0. Однако sin x и cos x не могут одновременно равняться нулю.

Поделив левую и правую части уравнение a sin x + b cos x = 0 cos x ≠ 0, получим a tg x + b = 0, после чего заканчиваем решения.

Пример 1. Решите уравнение 2 sin x - 7 cos x = 0.

Решения. Поделим обе части уравнения на cos x ≠ 0. Получим

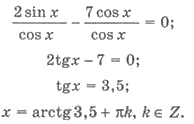
Тригонометрическое уравнение 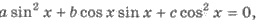где а, b, с - числа, из которых хотя бы два отличные от нуля, называют однородными тригонометрическими уравнениями второго степени относительно sin x и cos x. Сумма показателей степеней у всех слагаемых при sin x и cos x равен двум.

Если а ≠ 0, то уравнение (по аналогии с однородным 1-й степени) решают, разделив на cos² x ≠ 0 с последующей заменой tg x = t. Если же а = 0, то выносим cos х за скобки и применяем прием известный нам из предыдущего пункта.

Пример 2. Решите уравнение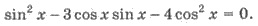

Решения. Те значения х, при которых cos x = 0 не являются корнями уравнения. Разделим левую и правую части уравнения на cos² x ≠ 0. Имеем

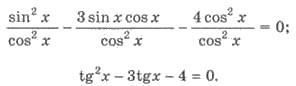
Замена tg x = t, имеем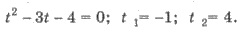

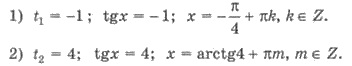
К однородным могут сводиться уравнения, которые имеют внешний вид, отличный от внешнего вида однородного уравнения. При этом часто применяют формулы тригонометрических функций двойного угла и тождество

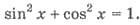
Пример 3. Решите уравнение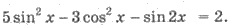

Решения. Применяем формулу sin 2x = 2 sin x cos x и такое тождество 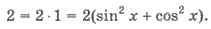Имеем

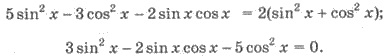
Поделим левую и правую части на cos² x ≠ 0. Имеем 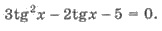Замена tg x = t. Уравнение 3t² -2t - 5 = 0 имеет корни t₁ = -1; t₂ = 5/3. Тогда