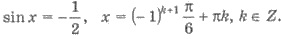АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел II. УРАВНЕНИЯ И НЕРАВЕНСТВА

§23. МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ.

2. Сведение тригонометрического уравнения к одной функции одного и того же аргумента.

Довольно часто после использования соответствующих тригонометрических формул удается свести уравнение к одной функции одного и того же аргумента, после чего применить замену переменных.

Если в уравнение входит только и tg х и ctg x, то после применения формулы ctg x = 1/tg x получим уравнение, содержащее только tg x.

Пример 1. Решите уравнение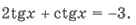

Решения. ОДЗ уравнения состоит из всех значений х, кроме тех, для которых cos x = 0 или sin x = 0. На ОДЗ уравнения имеем ctg x = 1/tg x. Запишем полученное уравнение

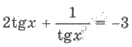и введем замену tg x = t. Имеем уравнение 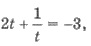когенями которого являются числа -1 и-1/2.

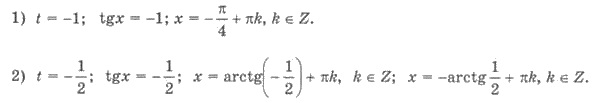
Если в уравнение входит только sin x и cos x, причем хотя бы одна из функций только в четных степенях (например, sin x), то применяем формулу sin² x = 1 - cos² х с последующей заменой cos х = t. Аналогично применяем формулу cos² x = 1 - sin² x, если cos х входит в уравнение только в четных степенях.

Пример 1. Решите уравнение

Решения. Так 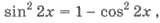то имеем

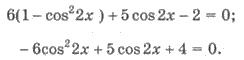
Делаем замену 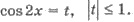Имеем

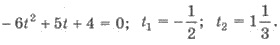
Второй корень не удовлетворяет уравнения, поскольку |t| ≤ 1.

Следовательно,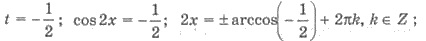

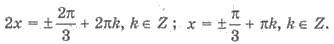
Если в тригонометрическое уравнение входят только cos 2x и cos x, то применяем формулу cos 2x = 2 cos² х - 1 и вводим замену cos x = t.

Если в тригонометрическое уравнение входят только cos 2x и sin х, то применяем формулу cos 2x = 1 - 2 sin² x и вводим замену sinx = t.

Пример 3. Решите уравнение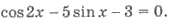

Решения. Имеем 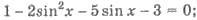замена

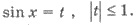
Уравнение 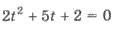имеет корни 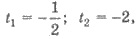с которых только первый удовлетворяет условию |t| ≤ 1. Следовательно,