Урок 20

Тема. Построение сечений многогранников

Цель урока: формирование умений учащихся применять свойства параллельных плоскостей к решению упражнений, построения сечений.

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания.

1. Три ученика воспроизводят решения задач № 28, 30, 31 на доске, в это время класс пишет математический диктант.

2. Математический диктант.

Через вершины А, В, С, D: вариант 1 - параллелограмма АВСD (рис. 76). Вариант 2 - трапеции АВСD (рис. 77), которые лежат в одной из параллельных плоскостей α, проведены параллельные прямые, пересекающие вторую плоскость β в точках А1, В1, С1, D1.

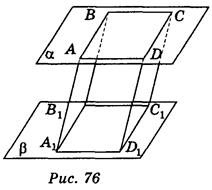
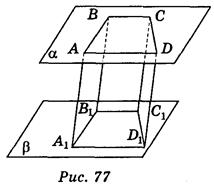
Пользуясь изображением, запишите:

1) прямую, которая лежит в плоскости β и параллельная прямой АС; (2 балла)

2) отрезки, длины которых равны АА1; (2 балла)

3) чему равен угол А1АD1, если АА1D1 = 120°; (2 балла)

4) чему равна длина диагонали ВD, если В1D1 = 3 см; (2 балла)

5) вид четырехугольника А1B1C1D1; (2 балла)

6) чему равна площадь четырехугольника А1В1С1D1, если площадь четырехугольника АВСВ равна 30 см2. (2 балла)

Ответ. Вариант 1. 1) А1C1; 2) ВВ1, СС1, DD1; 3) 60°; 4) 3см; 5) параллелограмм; 6) 30 см2.

Вариант 2. 1) А1C1; 2) ВВ1, СС1, DD1; 3) 60° ; 4) 3см; 5) трапеция; 6) 30 см2.

3. Проверка выполнения математического диктанта, заслушивания решения задач № 28, 30, 31 и ответы на вопросы учащихся, возникшие в процессе решения этих задач.

II. Закрепление и осмысление знаний учащихся

Формирование умений учащихся строить сечения многогранников, используя свойства параллельных плоскостей

Свойство параллельных плоскостей широко применяется при решении задач, в частности задач на построение сечений.

Задача.

Построить сечение прямоугольного параллелепипеда АВСDА1B1C1D1 плоскостью α, проходящей через вершины А, С и внутреннюю точку М ребра А1В1 (рис. 78).

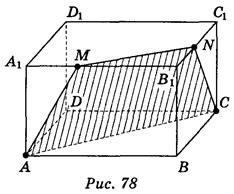
Решение

Сечение плоскости α с двумя гранями получим, построив отрезки АС ТАМ. Поскольку плоскости граней АВСD и А1В1С1D1 параллельны, то параллельны и их линии пересечения с плоскостью α, поэтому, построив МN || АС и отрезок МС, получим сечение - трапецию АМКС.

Решение задач

1. В треугольной пирамиде SАВС провести сечение:

а) через середину ребра АС параллельно грани SСВ;

б) через середину ребра SС параллельно грани SАВ.

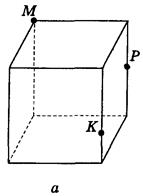
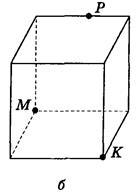
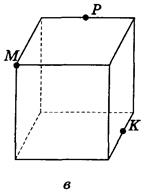
Рис. 79

2. Постройте сечение куба плоскостью, проходящей через точки М, К, Г (рис. 79).

3. Дан куб ABCDA1B1C1D1. Постройте сечение куба плоскостью, проходящей через данные точки: а) С1, К, D; б) С1, К, С, где точка К - середина А1В1. Выясните, какая фигура образуется в сечении. (Ответ а) равносторонняя трапеция; б) прямоугольник.)

4. Точка Х делит ребро АВ куба ABCDA1B1С1D1 в отношении АХ : ХВ = 2 : 3. Постройте сечение этого куба плоскостью, которая параллельна плоскости АА1С1 и проходит через точку X. Найдите периметр сечения, если АВ = а. (Ответ. .)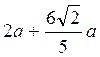

5. Докажите, что когда сечением параллелепипеда е шестиугольник, то его противоположные стороны параллельны.

6. Может сечением куба быть правильный пятиугольник?

7. Постройте сечение куба плоскостью, которая проходит через точку Е и параллельна плоскости MNP (рис. 80).

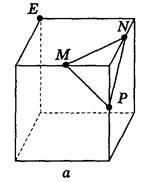
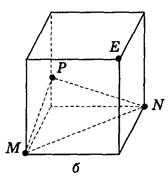
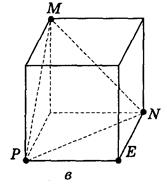
Рис. 80

8. Постройте прямоугольный параллелепипед ABCDA1B1C1D1 и его сечение плоскостью, проходящей через: а) ребро СС1 и точку пересечения диагоналей грани AA1D1D; б) точку пересечения диагоналей грани ABCD и параллельно плоскости АВ1С1.

9. Точка А1 делит ребро SA тетраэдра SABC в отношении SA1 : A1A = 2 : 3. Постройте сечение тетраэдра плоскостью, проходящей через точку А1 и параллельна плоскости АВС. Найдите периметр и площадь сечения, если АВС - правильный треугольник и АВ = 10 см. (Ответ. 12 см; 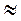7 см2.)

III. Домашнее задание

Решить следующую задачу.

Дан куб ABCDA1B1C1D1. Докажите, что сечение куба плоскостью А1С1К, где К - середина DC, есть трапеция, а сечения куба плоскостями А1В1К и АА1К есть паралелограмами.

IV. Подведение итога урока

Устное решение задач

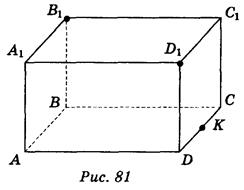
1. ABCDA1B1C1D1 - прямоугольный параллелепипед. Докажите, что сечение прямоугольного параллелепипеда плоскостью, проходящей через точки В1, D1 и К, где точка К - середина ребра CD, есть трапеция (рис. 81).

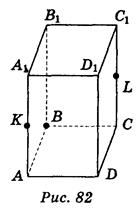
2. ABCDA1B1C1D1 - прямоугольный параллелепипед (рис. 82). Докажите, что сечение его плоскостью, проходящей через точки В, К, L, где точка К - середина ребра AA1, а точка L - середина ребра СС1, есть параллелограмм.