Урок 19

Тема. Решение задач

Цель урока: формирование умений учащихся применять свойства параллельных плоскостей к решению задач.

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания

1. Два ученика воспроизводят решения задач № 29, 32.

2. Фронтальное опрашивание.

1) Сформулируйте свойство линий пересечения двух параллельных плоскостей третьей плоскостью.

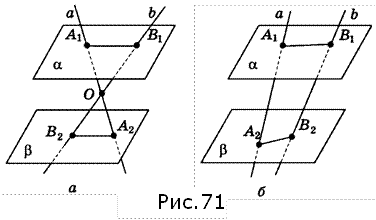
2) Точка О лежит между параллельными плоскостями α и β (рис. 71а). Две прямые а и b, которые проходят через точку А, пересекают плоскость α в точках A1, B1, а плоскость β - в точках А2, В2. Укажите, какие из утверждений правильные, а какие - неправильные:

а) если А1В1 = А2В2, то обязательно А1В2 = В1А2;

б) прямые А1В1 и А2B2 скрещивающиеся;

в) прямые A1B1 и a2B2 параллельные;

г) прямые а и b лежат в одной плоскости.

3) Плоскости α и β параллельны. Скрещивающиеся прямые а и b пересекают плоскость α в точках А1, В1, а плоскость β - в точках А2, В2 (рис. 71б). Укажите, какие из утверждений правильные, а какие - неправильные:

а) прямые А1В2 и В1А2 пересекаются;

б) прямые А1В1 и А2В2 параллельные;

в) прямые А1В2 и А2В1 лежат в одной плоскости;

г) через точки А1, А2, В1, В2 можно провести плоскость.

4) Сформулируйте свойство параллельных отрезков, которые лежат между параллельными плоскостями.

3. Проверить правильность выполнения учащимися задач № 29, 32 и ответить на вопросы, которые возникли у учащихся при решении этих задач.

II. Закрепление и осмысление знаний учащихся

Решение задач

1. Равные треугольники АВС и А1В1С1 размещены в плоскостях α и β так, что прямые АА1, ВВ1, СС1 параллельны. Следует ли из этого, что плоскости α и β параллельны?

2. Докажите, что отрезки параллельных прямых, которые лежат между плоскостью и параллельной ей прямой, равны.

3. Докажите, что два угла с соответственно параллельными сторонами либо равны, либо их сумма равна 180°.

4. Задача № 35* из учебника (с. 22).

Решение

Пусть прямая а пересекает плоскость α1 в точке X1, плоскость α2 - в точке Х2, плоскость α3 - в точке Х3 (α1 || α2 || α3) (рис. 72). Пусть вторая прямая b пересекает плоскость α1 в точке Y1, плоскость α2 - в точке Y2, плоскость α3 - в точке Y3. Проведем прямую с через точку X1, так что с || b. Пусть прямая с пересекает плоскость α2 в точке Z2, а плоскость α3 - в точке Z3. ΔХ1Х2X3 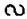ΔX1X3Z3, тогда Х1Х2 : Х2Х3 = Х1Z2 : Z2Z3. Но Х1Z2 = Y1Y2, Z2Z3 = Y2Y3. Поэтому Х1Х2 : Х2Х3 = Y1Y2 : Y2Y3. Таким образом, отношение Х1Х2 : Х2Х3 = Y1Y2 : Y2Y3 не зависит от выбранной прямой, то есть одинаковое для любых прямых.

5. Задача № 36 из учебника (с. 22).

Решение

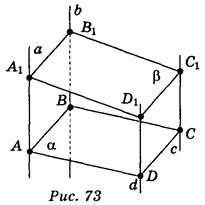
Пусть α не параллельна β. Прямые а, b, с, d - параллельны между собой (рис. 73). Плоскость α пересекает их в вершинах параллелограмма АВСD, а плоскость β пересекает эти прямые в точках А1, В1, С1, D1. Докажем, что А1В1С1D1 - параллелограмм. Плоскости ABB1A1, и DCC1D1 параллельны между собой, потому что АВ || DС, ВВ1 || СС1. Эти две параллельные плоскости пересекает плоскость β по прямым А1В1 и D1С1, поэтому А1В1 || С1D1. Аналогично доказываем, что А1D1 || В1С1. Таким образом, А1В1C1D1 - параллелограмм.

III. Домашнее задание

§2, п. 12; контрольные вопросы № 10, 11; задачи № 28, 30, 31 (с. 21).

IV. Подведение итога урока

Устное решение задач

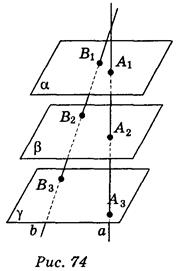
1. Прямые а и b, которые имеют общую точку, пересекают три даны параллельные плоскости α, β, γ в точках A1, А2, A3 и В1, В2, В3 соответственно (точка А2 лежит между точками А1 и А3, а точка2 - между точками В1 и В3) (рис. 74). Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) прямые А1В2 и А2В3 скрещивающиеся;

б) прямая а и точки В1 и В3 обязательно лежат в одной плоскости;

в) если А1А2 = 25 см, В2В3 = 4 см, А2А3 + В1В2 = 20см, то В1В3 = 14 см;

г) А1А3 : А1А3 = В1В2 : 1B2.

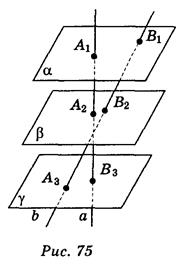
2. Три параллельные плоскости α, β, γ пересекают скрещивающиеся прямые а и b в точках А1, А2, А3 и В1, В2, В3 (плоскость β лежит между плоскостями α и γ) (рис. 75). Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) прямые А1В2 и А2В3 могут быть параллельными;

б) прямые В1А2 и В2А3 могут пересекаться;

в) А1А2 : А2A3 = 1B2 : В2B3;

г) А1А3 : В1В2 = А1А2 : 1В3.