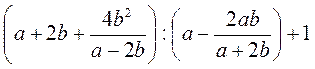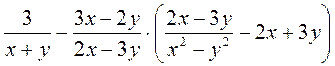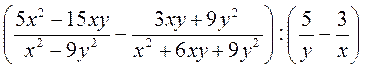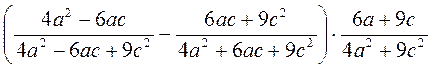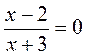|
@ Изучения материала урока начинается с систематизации знаний учащихся по видам уравнений с одной переменной и дополнение знаний учащихся о видах уравнений представлениям о общий вид рациональных уравнений, а также разновидностей таких уравнений (целых и дробных). При этом важно, чтобы учащиеся осознали, что именно вид выражений, из которых состоит данное уравнение, и определяет вид уравнения, который в свою очередь определяет способ решения уравнения. На этом уроке начинается кропотливая работа по формированию устойчивых умений учащихся решать дробные уравнения путем равносильных преобразований, по общей схеме, представленной в Таблицах по алгебре, 7-11 классы» Есть. П. Нелина, которая предполагает прежде всего понимание учащимися содержания понятия «ОДЗ уравнения». Поэтому для формирования у учащихся умения математически грамотно решать дробные уравнения правильно было бы уже на первых уроках знакомства учащихся с новым для них видом уравнений, отталкиваясь от знакомого учащимся понятие ОДЗ выражения, сформировать определение ОДЗ уравнения и на примерах продемонстрировать, как влияет изменение ОДЗ (переход от целого уравнения с дробной) на количество и возможность существования корней уравнения (такой подход к изложению вопроса о решение дробно-рациональных уравнений в 8 классе целесообразно осуществлять при условии надлежащего уровня интеллектуальной подготовки учащихся). Далее целесообразно было бы составить с учащимися алгоритм нахождения ОДЗ простейшего дробного рационального уравнения вида
(где А и В - некоторые многочлены от одной переменной). В 8 классе традиционно изучается несколько способов равносильного преобразования дробных уравнений, но на первом уроке, чтобы не перегрузить учащихся новыми понятиями, к рассмотрению предлагается способ решения дробных уравнений, который предусматривает использование условия равенства дроби нулю. * Если позволяет уровень подготовки учащихся (сформированы четкое представление о содержании понятия уравнения с параметром и умение решать линейные уравнения с параметрами), то уже на этом уроке можно предложить учащимся ознакомиться со схемой решения дробно-рациональных уравнений с параметром.
VI. Усвоение знаний Выполнение устных упражнений 1. Какие из уравнений: 2х - 1 = 0; х2 - 3х + 5 = 0; 2. Прокомментируйте (используя алгоритм) решения уравнения 1) ОДЗ: х ≠ 0 и х + 1 ≠ 0; х ≠ 0 и х ≠ -1; 2) 3) х - 1 = 0, х = 1 - входит в ОДЗ. Ответ. 1. 3. Заполните таблицу:
Выполнение письменных упражнений Для реализации дидактической цели урока следует решить задачи следующего содержания: 1*. Нахождение ОДЗ дробно-рационального уравнения вида 2. Проверка по известным ОДЗ уравнения, которые из заданных чисел не являются корнями уравнения (не входят в ОДЗ). 3. Решение дробно-рациональных уравнений вида 1) Решите уравнение: а) 2) Решите уравнение: а) 3) Решите уравнение: а) 4. Составление и решение уравнений по словесному описанию. 1) Какое число надо прибавить к знаменателю дроби 2) Какое одно и то же число надо добавить в числитель дроби 5. Составление и решение уравнений по условию задачи. Знаменатель дроби на 3 больше числителя. Если в числитель дроби прибавить 32, то получим дробь, вдвое больше данного. Найдите начальный дробь. 6*. Решение дробно-рациональных уравнений с параметром. Решите уравнение с параметром а: 7. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) При каком значении а тождественно равные выражения 2) Какое число пропущено?
8. На повторение: преобразуйте рациональное выражение с использованием приобретенных ранее знаний. Упростите выражение: а) б) в) г) @ Упражнения для письменного решения, предложенные на урок, предусматривают формирование умений использовать алгоритм решения дробно-рациональных уравнений, рассмотренный выше, поэтому представляют достаточно большое количество рациональных уравнений; но, чтобы разнообразить работу учащихся на уроке, упражнения на решение уравнений можно дополнить упражнениями на составление уравнений или по описанию соотношение выражений, из которых состоит уравнения (на этом этапе можно провести работу по составлению всех возможных видов уравнений для данной записи соотношения выражений), или по условию арифметической задачи. Также упражнения урока можно дополнить упражнениями на повторение предыдущего материала (преобразование рациональных выражений). @ *Если позволяет уровень подготовки учащихся (с целью долгосрочной подготовки к независимому внешнему оцениванию учащихся в 12 классе), можно предложить к решению серию простейших дробно-рациональных уравнений с параметром (изучив предварительно соответствующий алгоритм).
VII. Итоги урока В любом из случаев правильно решенное уравнение?
VIII. Домашнее задание 1. Изучить определение рационального уравнения, целой рационального уравнения, дробно-рационального уравнения, ОДЗ рационального уравнения, алгоритм решения дробно-рационального уравнения вида 2. Решить упражнения на применение изученного алгоритма разного уровня сложности. 3. Повторить свойства равносильных уравнений, основное свойство пропорции; развязали серию уравнений на применение этих свойств (см. 6, 7 классы).
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
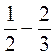 ;
; 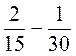 ;
; 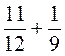 ;
; 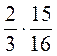 ;
; 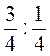 ;
; 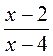 ;
; 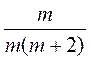 ;
; 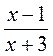 ;
; 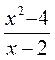 ;
; 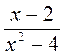 .
.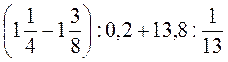 ; б)
; б) 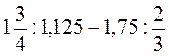 ; в)
; в) 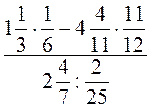 .
.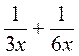 ; б)
; б) 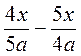 ; в)
; в) 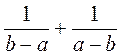 ; г)
; г) 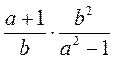 ; д)
; д) 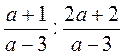 .
.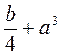
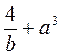
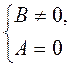 (найти, какие из корней уравнения А = 0 удовлетворяют ОДЗ уравнения);
(найти, какие из корней уравнения А = 0 удовлетворяют ОДЗ уравнения);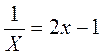 ;
; 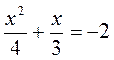 ;
; 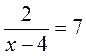 являются рациональными? целыми рациональными? дробно-рациональными?
являются рациональными? целыми рациональными? дробно-рациональными?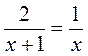 .
.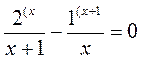 ,
, 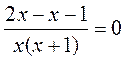 ,
, 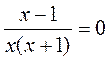 ;
;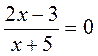
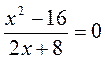
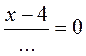
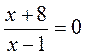 ; б)
; б) 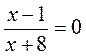 ; в)
; в) 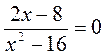 .
.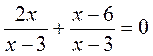 ; б)
; б) 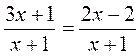 ; в)
; в) 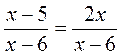 .
.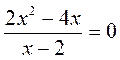 ; б)
; б) 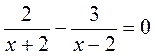 ; в)
; в) 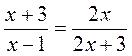 .
.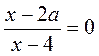 .
.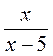 и
и 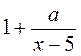 ?
?