|
Понятно, что эффективной эта работа может быть только в случае дальнейшей коррекции. Для учеников, которые хорошо освоили приемы работы с выражениями, которые выносятся на контроль на нем этапе урока, учитель может предложить дополнительные задания именно такого типа и оценить их выполнение.
III. Формулировка мсти и задач урока Проведена проверка выполнения домашнего задания и анализ возможных ошибок сами по себе создают мотивацию учащихся к деятельности по устранению причины ошибок (коррекции знаний), а также совершенствования умений (формирование навыков). Достижения наилучших результатов этой деятельности - коррекция знаний и отработки умений учащихся выполнять преобразование рациональных выражений с применением изученных алгоритмов выполнения арифметических действий с рациональными дробями - и составляет основную дидактическую месть за урока.
IV. Актуализация опорных знаний и умений @ С целью успешного восприятия учащимися учебного материала перед изучением материала урока следует активизировать такие знания . и умения учащихся: правила выполнения арифметических действий с рациональными числами и порядок выполнения действий в числовых выражениях, содержащих действия различной степени; тождественные преобразования целых выражений; преобразование суммы, разности, произведения и доли двух рациональных дробей на рациональный дробь, а также преобразование рационального дроби с применением основного свойства рационального дроби (возведение рациональной дроби к новому знаменателю, возведение нескольких рациональных дробей к новому наименьшего общего знаменателя). Учитывая дидактическую цель (ударение на коррекционной работе) и с целью разнообразия форм работы на уроке, можно предложить ученикам на этом этане урока провести блицопрос (или провести интерактивное упражнение «Микрофон»); главное условие - четкий и краткий ответ на вопрос. Вопрос 1. Как формулируется основное свойство дроби? 2. Что произойдет со знаком дроби, если заменить знак его числитель; знаменатель; числителя и знаменателя? 3. Как добавить дроби с одинаковыми знаменателями? 4. Как выполнить вычитание дробей с одинаковыми знаменателями? 5. Как добавить дроби с разными знаменателями? Расскажите на примере дроби: а) 6. Как выполнить умножение двух дробей? 7. Какое вы знаете правило подъема дроби в степень? 8. Сформулируйте правило деления дробей. 9. Расскажите о порядке преобразования выражений: а)
V. Формирование умений Выполнение устных упражнений 1. Подайте в виде несократимый дроби выражение: а) 2. Назовите наименьший общий знаменатель дробей (выражений): а) 3. При каких значениях переменной значение дроби равно нулю?
Выполнение письменных упражнений На уроке коррекции знаний и отработки навыков логично будет предложить учащимся решить упражнения примерно такого содержания: 1. Преобразование рационального выражения на рациональный дробь (по общей схеме, составленной на уроке 17). 1) Упростите выражение: а) 2) Упростите выражение: а) 3) Упростите выражение: 4) Выполните действия: 5) Упростите выражение: г) 2. Представление отношения дробных рациональных выражений в виде отношения многочленов (с применением основного свойства дроби). 1) Представьте в виде рациональной дроби: 2) Найдите значение выражения: а) 3) Представьте в виде рациональной дроби: а) 3. Доказательства того, что значение выражения не зависит от значения переменной. 1) Докажите, что при всех допустимых значениях букв значение выражения 2) Докажите, что при любом натуральном n значение выражения 4. Доказательства тождеств. а) б) 5. Упражнения на повторение (особенно на нахождение ОДЗ рационального выражения и отыскания значения переменных, при которых значение выражения равно нулю). 6. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) Представьте в виде рациональной дроби выражение: а) 2) Докажите, что при всех допустимых значениях переменных значение выражения 3) выражение пропущено?
@ Как было сказано выше, задачи на преобразование рациональных выражений на рациональный дробь в общем случае является достаточно сложной задачей, поскольку предполагает свободное овладение алгоритмами выполнения различных арифметических действий с рациональными дробями, а также достаточно высокий уровень умений применять эти алгоритмы на практике и переключаться с одного алгоритма на другой. Поэтому уровень сложности заданий учитель выбирает в зависимости от уровня знаний и умений учащихся, не занижая требования к ученикам, но в то же время создавая ситуацию успеха. С целью подготовки учащихся к восприятию следующего раздела («Рациональные уравнения») следует продолжить решать упражнения на нахождение ОДЗ рационального выражения и отыскания значения переменных, при которых значение выражения равно нулю.
VI. Итоги урока Самостоятельная работа № 5
VII. Домашнее задание 1. Повторить алгоритмы выполнения арифметических действий с рациональными дробями. 2. Решить упражнения содержания, аналогичного упражнениям самостоятельной работы можно предложить упражнения противоположного варианта). 3. Повторить: определение рационального целого рационального и дробного рационального выражений ОДЗ рационального выражения; определение уравнения, свойства равносильности уравнений, понятие линейного уравнения с одной переменной и алгоритм решения линейного уравнения; решить линейные уравнения (в том числе и уравнения с параметрами); повторить содержание понятия «пропорция» и основное свойство пропорции, решить несколько уравнений на применение этого свойства (см. 6 класс).
|
| ||||||||||||||||||||||||||||||||||||
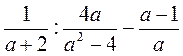 ; б)
; б) 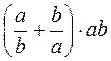 ; в)
; в) 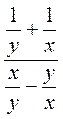 .
.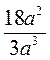 ; б)
; б)  ; в)
; в) 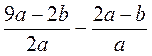 ; г)
; г) 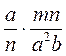 ; д)
; д) 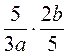 ; е)
; е) 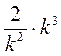 ; ж)
; ж) 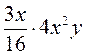 ; з)
; з) 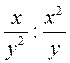 ; и)
; и) 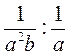 ; к)
; к) 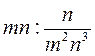 ; л)
; л) 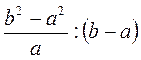 .
.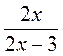 ;
; 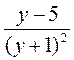 ;
; 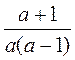 ;
; 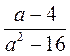 .
.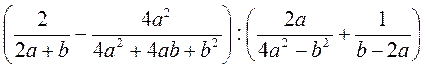 ; б)
; б) 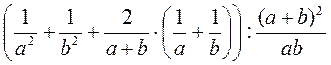 ; в)
; в) 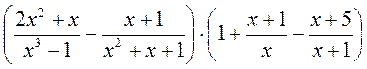 .
.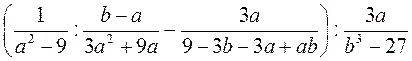 ; б)
; б) 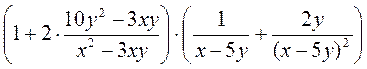 ; в)
; в) 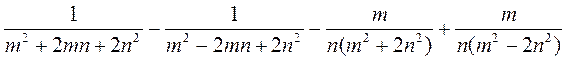 .
.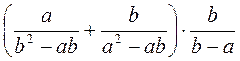 ; б)
; б) 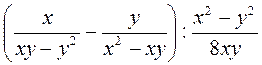 ; в)
; в) 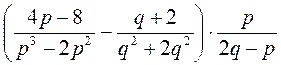 ; г)
; г)  .
.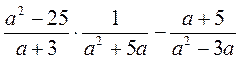 ; б)
; б) 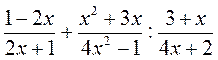 ; в)
; в) 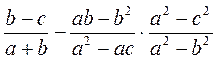 ; г)
; г) 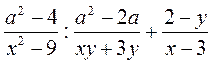 .
.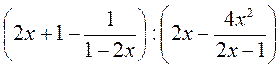 ; б)
; б) 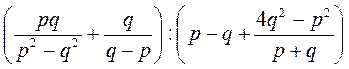 ; в)
; в) 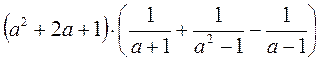 ;
; 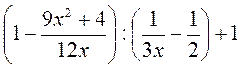 ; д)
; д) 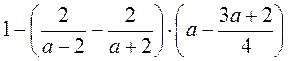 ; е)
; е) 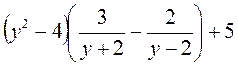 .
. .
.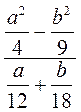 при а =
при а = 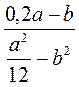 при а = -8,
при а = -8, 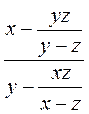 ; б)
; б) 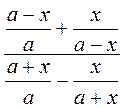 ; в)
; в)  ; г)
; г) 
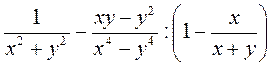 равно 0.
равно 0.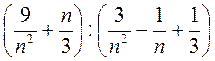 является натуральным числом.
является натуральным числом.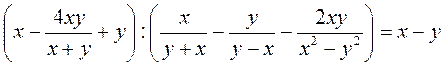
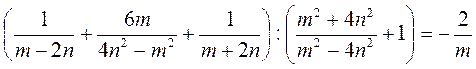
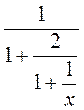 ; б)
; б) 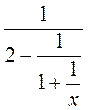
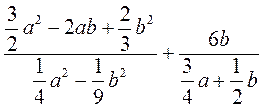 не зависит от а и
не зависит от а и 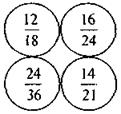
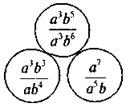

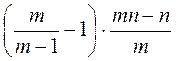 ;
; 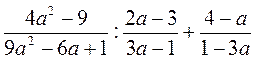 ;
;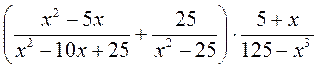 ;
; 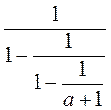
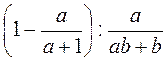 ;
; 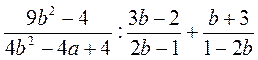 ;
; 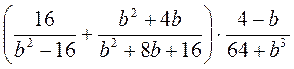 ;
;