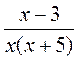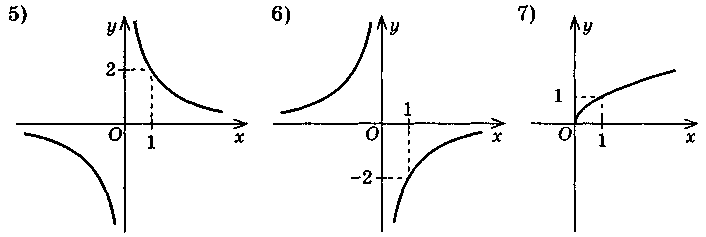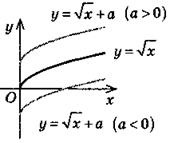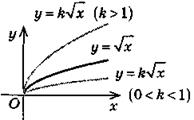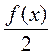УРОК № 20
Тема. Простейшие преобразования графиков функций
Цель урока: сформировать понимание учащимися содержания понятия «преобразование графика функции», а также понимание того факта, что определенное преобразование уравнения функции влечет за собой преобразование графика и наоборот. Сформировать знания учащихся об основных видах геометрических преобразований графиков функций (на интуитивном уровне) и о уравнение для функции, задаваемой этим преобразованием. Сформировать первичные умения «читать» графики функций (то есть за готовыми графиками задавать уравнения функций), а также выполнять построения графиков функций с помощью преобразований, заданных уравнением данной функции.
Тип урока: формирование знаний и первичных умений.
Наглядность и оборудование: опорный конспект № 14, раздаточный материал (карточки с решениями домашних упражнений).
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Для экономии времени на уроке в случае необходимости учитель может предложить ученикам раздаточный материал - решения домашних упражнений - самостоятельно проработать дома.
Для организации текущего контроля за усвоением учащимися знаний и умений можно предложить им тестовые задания (см. ниже), проверка которых проводится сразу после выполнения. Учитель фиксирует фамилии тех учеников, которые требуют дополнительного педагогического внимания для возможности осуществления определенной коррекционной работы.
Тестовые задания
1. На рисунке изображен график функции, область определения которой D(f) = R. Правильным является утверждение:
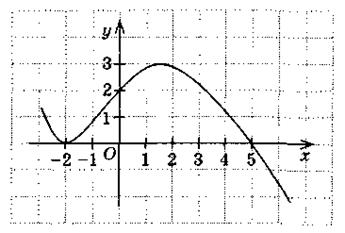
а) нули функции: 2; 2,5; f(x) возрастает, если х  [-2; 3]; f(x) 0, если x
[-2; 3]; f(x) 0, если x  (5; +∞);
(5; +∞);
б) нули функции: 2; 5; f(x) возрастает, если x  [-2; 2]; f(x) 0, если х
[-2; 2]; f(x) 0, если х  [5; +∞);
[5; +∞);
в) нули функции:-2; 5; промежуток возрастания x  [-2; 2]; f(х) 0, если х
[-2; 2]; f(х) 0, если х  (5; +∞);
(5; +∞);
г) нули функции: 3; промежутке роста нет; f(x) 0, если x  (-∞; -2) и x
(-∞; -2) и x  (2; +∞).
(2; +∞).
2. Область определения функции у = 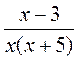 :
:
а) х 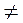 5;
5;
б) х 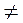 -5;
-5;
в) х 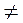 -5, х
-5, х 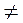 0;
0;
г) х 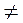 3.
3.
3. Область значений функции f(x) = x2 - 3:
а) (-∞; +∞);
б) [3; +∞);
в) [-3; +∞);
г) (-3; +∞).
4. Если f(x) = 3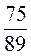 х - 1, то:
х - 1, то:
а) f (3) f (4);
б) f (3) > f (4);
в) f (3) f (4);
г) f (3) = f (4).
5. Значение функции у(х) = -3х + 8 положительные, если:
а) х ≤ 2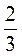 ;
;
б) х ≥ 2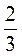 ;
;
в) х 2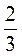 ;
;
г) таких значений х нет.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
На этом этапе урока уместными будут слова учителя о том, что исследование функций с готовым графиком является более простым, чем по формуле (подтверждением этой мысли могут стать результаты проверки тестовых заданий). Развивая эту мысль, учитель сообщает ученикам о том, что в ряде случаев для решения задач бывает необходимо построить график функции, которая не является элементарной (учитель может привести ряд примеров таких функций). Итак, формулируется вопрос: существуют ли средства (и если существуют, то как ими пользоваться), с помощью которых можно построить график некоторой функции, используя при этом умение строить графики элементарных функций (линейной, обратной пропорциональности, квадратичной функции и функции у = 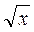 ). Понятно, что поиск ответа на поставленный вопрос и является основной дидактической целью урока.
). Понятно, что поиск ответа на поставленный вопрос и является основной дидактической целью урока.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Какая из приведенных функций является возрастающей:
а) на области определения;
б) на промежутках (-∞; 0) и (0; +∞)?
1) у = 4х - 1;
2) у = 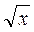 ;
;
3) у = -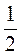 x + 1;
x + 1;
4) у = 3х;
5) у = 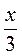 ;
;
6) у = х2;
7) у = -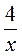 .
.
2. Графиком какой из приведенных функций является прямая, проходящая через начало координат? Объясните свой ответ, не выполняя построения:
1) у = 2х + 1; 2) у = 2х; 3) у = 2х2; 4) у = 2; 5) у =  ; 6) у =
; 6) у = 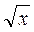 .
.
3. На одном из рисунков изображен график функции у = 2х. Укажите этот рисунок.
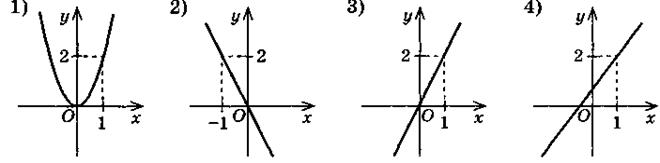
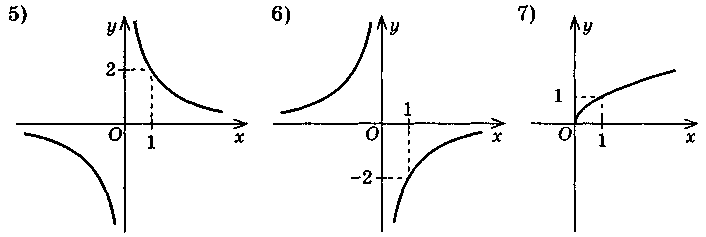
4. Для функции f(x) = x2 - 3 найдите значение выражения:
1) f (-2); 2) f (-1); 3) f (0); 4) f (1); 5) f (2); 6) f (3); 7) f (4); 8) f (5); 9) f (6).
V. Формирование знаний
План изучения нового материала
1. Представление о преобразования графика функции.
2. Построение графиков параллельным переносом вдоль оси ординат (оси).
3. Построение графика функции симметрией относительно оси абсцисс.
4. Растяжения (сжатия) графика функции вдоль оси ординат.
Опорный конспект №14
Простейшие преобразования графиков функций |
№ п/п |
Формула зависимости |
Пример |
Преобразования |
1 |
y = -f(х) |
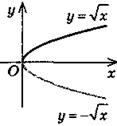
|
Симметрия относительно оси Ох |
2 |
y = f(х) + a |
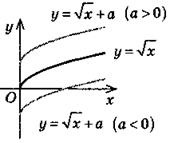
|
Параллельный перенос вдоль оси Оу на а единиц (если а > 0, то вверх, если а 0, то вниз) |
3 |
y = f(х + a) |
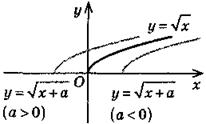
|
Параллельный перенос вдоль оси Ох на а единиц (если а > 0 - влево, если а 0 - вправо) |
4 |
y = kf(х) (k > 0) |
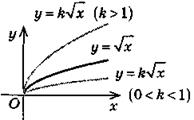
|
Тот же вид, что и y = f(x), только растяжение-нуто, если k > 1, и сжат, если 0 k 1 |
Методический комментарий
Сразу следует заметить, что изучение вопроса о геометрические преобразования графиков функций на данном уроке является достаточно сложным через определенное несоответствие программ изучения геометрии и алгебры в 9 классе. Это несоответствие существовала в ранее действующей программе и, к сожалению, сохранилась в программе для 12-летней школы. Поэтому формирование представления о геометрических преобразованиях графиков функций производится на данном уроке на интуитивном уровне, и учителю не следует акцентировать внимание на строгих определениях выделенных им видов преобразований. Основное внимание уделяется, установлению и усвоению учащимися связи между уравнением функции и определенным видом преобразования графика функции (эта связь отражено в опорном конспекте № 14). Изучение связи между видом преобразования и уравнение функции, как это происходило последние годы, производится через вычисление значений функции в отдельных точках и наблюдения за изменением значений функции в этих точках в зависимости от изменения вида функции. Результаты данных «наблюдений» имеют вид таблицы (см. опорный конспект № 14).
VI. Формирование умений
Устные упражнения
1. Как нужно преобразовать график функции y = f(x), чтобы образовался график функции:
1) y = -f(x);
2) y = f(x + 2);
3) y = f(x - 2);
4) y = f(x) + 2;
5) y = f(x) - 2;
6) y = 2f(x);
7) y = 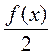 ?
?
2. Даны графики функций:
a) y = xa; б) y = 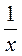 ; в) у =
; в) у = 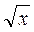 .
.
Какое уравнение будет иметь функция, график которой образуется из данных графиков функций: 1) при параллельном переносе вверх на 3 единицы; 2) при растяжении в 3 раза; 3) при параллельном переносе вправо на 3 единицы?
Письменные упражнения
Содержание упражнений, предлагаемых к решению на уроке, может быть таким:
1) среди заданных графиков функций выбрать те, что соответствуют данным уравнением;
2) построить график функции, заданной уравнением, выполнив соответствующее уравнение геометрическое преобразование;
3) на повторение: исследовать функцию, заданную графически, на монотонность, найти ее нули, промежутки возрастания и убывания, область значений.
(Задачи на построение графиков функций путем геометрических преобразований на данном уроке имеют начальный или средний уровень сложности.)
Методический комментарий
Формированию устойчивых умений выполнять построение графиков функций путем преобразований графиков элементарных функций должно предшествовать работа с повторения вопросов о видах и особенностях графиков элементарных функций (эта работа проводилась в течение последних четырех уроков). Формирование умения выполнять построение графика функции путем геометрических преобразований ведется параллельно с закреплением знаний учащихся о формулы, соответствующие этим преобразованиям. Поэтому при выполнении как устных, так и письменных упражнений на этом и следующем уроках учителю следует требовать от учеников в первую очередь анализа формулы данной функции, а потом уже выбора в соответствии с ней геометрического преобразования , для построения графика функции. Такой подход, во-первых, способствует более быстрому усвоению учащимися содержания учебного материала урока, а во-вторых, помогает предупредить ошибки, которые часто возникают у учащихся, особенно, когда речь идет о параллельном переносе вдоль разных координатных осей.
VII. Итоги урока
Контрольный вопрос
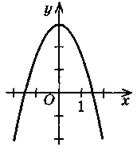
График какой функции изображен на рисунке?
1) у = х2 + 3;
2) у = х2 - 3;
3) у = -х2 + 3;
4) у = -х2 - 3.
VIII. Домашнее задание
1. Освоить содержание изученных на уроке преобразований и соответствующих формул.
2. Решить упражнения на применение этих преобразований (уровень сложности и содержание соответствуют упражнениям, решенным на уроке).
3. На повторение: упражнения на нахождение области определения функции, нулей функции, промежутков возрастания /убывания функции.