Урок № 2
Тема. Луч (півпряма)
Цель: добиться усвоения
учениками определение луча, доповняльних півпрямих и понятие «определение некоторого
объекта»; добиться овладения учащимися умением обозначать и различать на рисунке
лучи, доповняльні лучи, выполнять рисунок по описанию ситуации с
использованием изученной терминологии.
Тип урока: усвоение знаний,
умений и навыков.
Форма проведения: фронтальная беседа.
Наглядность и
оборудование: таблица
«Луч».
ХОД УРОКА
И. Организационный
момент
Учитель проверяет
готовность учащихся к уроку, сообщает тему урока.
II.
Проверка домашнего задания
Математический
диктант
Вариант 1
1. Назовите какую-нибудь
геометрическую фигуру.
2. Выполните
изображение точки и обозначьте ее.
3. Начертите прямую и
отметьте ее.
4. Сколько совместных
точек имеют две прямые, которые не пересекаются?
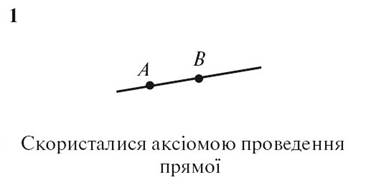
5. Начертите прямую a и
отметьте на ней точки A, B и C так, чтобы точка C лежала между точками A и B.
Вариант 2
1. Выполните
изображение точки и обозначьте ее.
2. Назовите какую-нибудь
геометрическую фигуру.
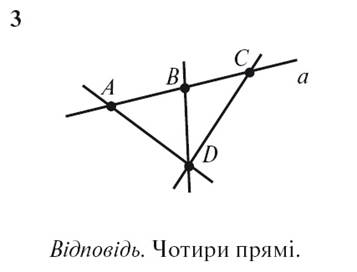
3. Могут ли две различные
прямые иметь две общие точки A и B?
4. Сколько совместных
точек имеют две прямые, которые пересекаются?
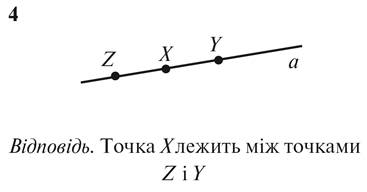
5. Начертите прямую b и
отметьте на нем точки M, N и P так, чтобы точка M лежала между точками N и P.
Методический комментарий
С целью коррекции
желательно после выполнения работы осуществить проверку (или с помощью
графопроектора или открыв работы двух учеников, которые работали за доской) и
продублировать более сложные задачи.
Решение
домашних упражнений проверяется учащимися по предложенным образцом.

III. Формулировка
цели и задач урока
Учитель формулирует в
адаптированном варианте основную дидактическую цель урока и после согласования с
учениками формулирует задачи урока.
IV.
Актуализация опорных знаний
Выполнение
устных упражнений
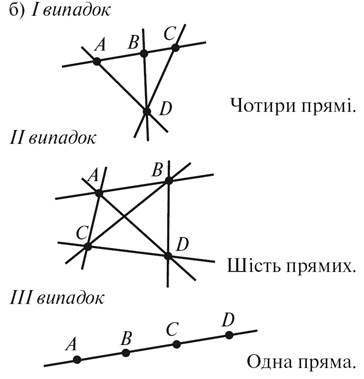
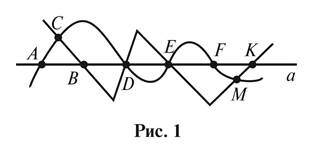
1. На рисунке 1 изображен
три линии: прямую, кривую и ломаную. Назовите точки, в которых пересекаются:
а) прямая и кривая;
б) прямая и ломаная;
в) кривая и ломаная;
г) все три линии.
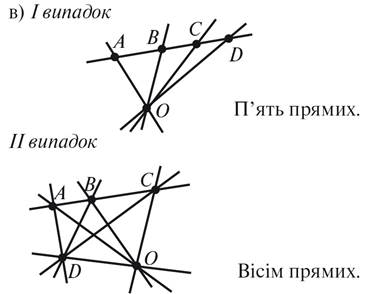
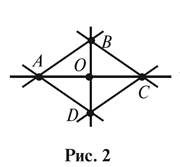
2. Назовите на рисунке
2:
а) прямые, которые не проходят
через точку C;
б) прямые, на которых
точка O лежит, а точка D не лежит;
в) прямые,
пересекаются в точке B, но не проходят через точку D;
г) произвольные три
точки, которые не лежат на одной прямой.
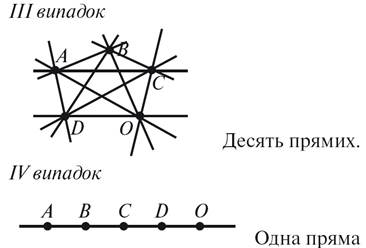
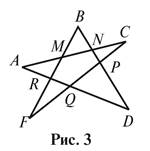
3.
На
рисунке 3 назовите:
а) точки, лежащие
между точками B и D;
б) точки, между которыми
лежит точка M;
в) точки, о которых
нельзя сказать,что они лежат между двумя другими;
г) пара точек,
лежат по одну сторону от точки P; по разные стороны от нее.
V.
Усвоение новых знаний
План изучения
нового материала
1°. Представление о разделении
прямой на части любой ее точкой.
2°. Определение луча;
его элементы.
3°. Доповняльні
лучи.
4°. Определение и его
роль в геометрии.
Методический комментарий
1°-3°. На уровне
интуитивного восприятия учащимся из курса математики 5 класса известны понятия луча
i доповняльних лучей. В этом пункте вводятся эти понятия с использованием
основного свойства расположения точек на прямой.
4°. Говоря о
определение и его роль в геометрии, желательно привести примеры различных определений, что
знакомы учащимся из курса математики 5-6 классов, и осуществить работу с определениями
по такой схеме: последовательно исключая из формулировки то или иное слово,
проводится анализ - будет изменено определение описывать тот объект, который мы
имеем в виду. В результате такой работы учитель подводит учащихся к выводу
о важности каждого слова в определении.
Как итог
обращаемся к таблице.
Таблица

IV.
Первичное осознание новых знаний
Выполнение
устных упражнений
1. Или правильное
утверждение?
«Через две различные
точки всегда можно провести луч, причем только один».
Ответ объясните.
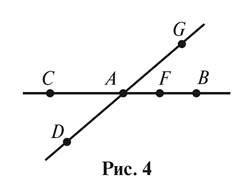
2. По рисунку 4 укажите:
а) все лучи,
изображенные на рисунке;
б) лучи с
начальной точкой F;
в) півпрямі с
начальной точкой A;
г) пары
доповняльних півпрямих;
д) лучи,
совпадают.
Выполнение графических
упражнений
Отметьте точку A.
а) Проведите
луч с началом A и отметьте на нем точку B. Назовите прямую, частью которой
есть луч AB.
б) Проведите
луч с початкомВ, что не проходит через точку A. можно назвать
построенный луч BA?
Выполнение
письменных упражнений
Уровень А
1. Отметьте точки A и B.
Проведите луч AB. Есть доповняльними лучи AB и BA?
2. На прямой обозначены
две точки. Сколько пар доповняльних променв при этом образовалось?
Уровень Б
1. Точка C лежит на
лучи AB, а точка B - на луче CA. Какая из этих трех точек лежит между двумя
другими?
2. Могут ли два
лучи одной прямой не быть доповняльними? Сделайте рисунок.
Уровень В
(дополнительно)
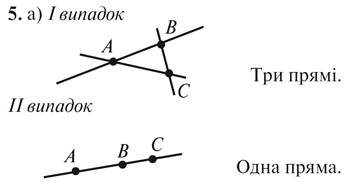
На прямой обозначены
точки A, B и C. Сколько различных лучей можно назвать с помощью этих точек?
Сколько среди этих лучей пар доповняльних лучей? Изменится ли ответ,
если данные точки не лежат на одной прямой?
Методический комментарий
На этом уроке, как
i на предыдущем, решая задачи, обращаем внимание учащихся на обоснование
действий, приучаем учеников до точных геометрических формулировок.
V. Итоги урока
1. На лучи MN обозначено
точку P. может Ли точка M лежать между точками N и P? Может ли точка N лежать между
точками M i P?
2. Лучи DK и DM-доповняльні.
Какая из точек D, K i M лежит между двумя другими?
VI. Домашнее
задача
Устно выполнить
упражнения.
1. На луче AB обозначено
точку C. может Ли точка A лежать между точками B и C? Может точкаВ лежать между
точками A и C?
2. Лучи DE и DF -
доповняльні. Какая из точек D, E и F лежит между двумя другими?
3. Два луча имеют
общую начальную точку. Или обязательно они есть доповняльними?
Письменно решить
задачи.
4. Постройте
доповняльні лучи PQ и PR. Назовите точки, лежащие по одну сторону от точки R.
Лежит ли точка Q на лучи RP?
5.
Точки
A, B и C лежат на одной прямой, причем лучи AB и AC не является доповняльними, а
точки A и C лежат по одну сторону от точки B. из этих трех точек лежит между
двумя другими?
6. Два луча имеют
единственную общую точку. Есть ли такие лучи доповняльними? Сделайте рисунки.
Дополнительная задача
На прямой обозначены
пять точек. Определите, какие из приведенных утверждений являются правильными:
а) любые три из
данных точек лежат между двумя другими;
б) среди данных
точек найдутся три, что лежат между двумя другими;
в) среди данных
точек существует по крайней мере одна, что не лежит между двумя из остальных этих точек;
г) среди данных
точек существует ровно одна, что не лежит между двумя из остальных этих точек.
Предлагаемая
дополнительная задача формирует у учащихся представление о содержании понятий «хотя бы один»,
«по крайней мере один», «ровно один» и т.д.
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.